Exo cosinus

[green day fan]

montrer que:

cos(pi/5)cos(3pi/5)=-1/4 :help:

svp aidez moi ca fait deux jours que je suis bloque

[zygomatique]

bonjour

merci

au revoir

...

[Pisigma]

montrer que:

cos(pi/5)cos(3pi/5)=-1/4 :help:

svp aidez moi ca fait deux jours que je suis bloque

comme le rappelait zygomatique un peu de politesse ne fait pas de tort :we:

Bonjour,

commence par développer en te rappelant la formule cos(a).cos(b)=....

[green day fan]

comme le rappelait zygomatique un peu de politesse ne fait pas de tort :we:

Bonjour,

commence par développer en te rappelant la formule cos(a).cos(b)=....

ah oui merci je croyais qu il se moquait de moi mon cher ami desole
mais meme si j ai developpé ca ne m a menait a rien :triste:

[Pisigma]

ah oui merci je croyais qu il se moquait de moi mon cher ami desole
mais meme si j ai developpé ca ne m a menait a rien :triste:

Tu peux nous montrer tes calculs?

[green day fan]

Tu peux nous montrer tes calculs?

oui voila:
cos(pi/5)cos(3pi/5)=1/2(cos(4pi/5)+cos(2pi/5))

[Pisigma]

oui voila:
cos(pi/5)cos(3pi/5)=1/2(cos(4pi/5)+cos(2pi/5))

Tu peux encore simplifier

[green day fan]

Tu peux encore simplifier

vous avez raison alors:
cos(pi/5)cos(3pi/5)=1/2(2cos^2(2pi/5)-1+cos(2pi/5))
=1/2((cos(2pi/5)(1+2cos(2pi/5)-1)

[Pisigma]

vous avez raison alors:
cos(pi/5)cos(3pi/5)=1/2(2cos^2(2pi/5)-1+cos(2pi/5))
=1/2((cos(frac2pi/5)(1+2cos(2pi/5)-1)

Je pensais a :



As-tu vu la formule de ?

[green day fan]

Je pensais a :



As-tu vu la formule de ?

non j ai pas reussi a trouver dsl
:mur:

[mathelot]

ici, rubrique cos(72°)
on trouve le calcul du cosinus de ° sous forme d'énoncé , mais sans les réponses

[green day fan]

ici, rurique cos(72°)
on trouve le calcul du cosinus de ° sous forme d'énoncé , mais sans les réponses

oui je sais merci :mur: :hein: :help:

[Pisigma]

non j ai pas reussi a trouver dsl
:mur:

en tenant compte de mon post précédent et des angles doubles, tu transformes



sachant que

si tu dois démonter "géométriquement", vois l'adresse suggérée par mathelot

[chan79]

on pose

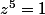
on a et donc

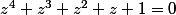
et

or et




ce qui donne bien -1/4 si on multiplie par 1/2

je ne sais pas si ça se fait au lycée ...

[mathelot]

bonjour,

est ce que c'est une question au milieu d' un énoncé ?
est ce qu'on suppose la valeur , avec un radical, de connue ?

(radicaux=racine carrée, cubique,etc..)

[green day fan]

on pose

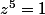
on a et donc

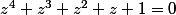
et

or et




ce qui donne bien -1/4 si on multiplie par 1/2

je ne sais pas si ça se fait au lycée ...

non merci tout de meme

[green day fan]

bonjour,

est ce que c'est une question au milieu d' un énoncé ?
est ce qu'on suppose la valeur , avec un radical, de connue ?

(radicaux=racine carrée, cubique,etc..)

non l exercise est tel que je l ai ecrit

[mathelot]

de
(racines 5eme de l'unité)


en projetant sur l'axe x'Ox, on obtient les abscisses des sommets du pentagone régulier:





d'après


ton produit vaut -1/4