Bonjour à tous,
Je suis en train de faire ma dérivée première sur cette fonction:
f(x) = (x-1)^2 (x+2)^2
et j'ai trouvé la dérivée suivante:
f'(x) = 4x^3 + 6x^2 - 6x - 4
Je dois à présent étudier sa croissance et donc trouver les zéros et je bloque:
4(x^3 - 1) + 6x(x - 1) = 0
Or je ne peux pas faire de regroupement après ma mise en évidence et tout doit être sous forme de produit pour pouvoir trouver les zéros.
Comment puis-je continuer? Le problème réside dans le fait que les polynômes dans les parenthèses ne sont pas les mêmes, je ne peux pas faire de regroupement.
Je sais par exemple que (x^2 - 1) = (x - 1) (x + 1) mais pour (x^3 - 1) je ne trouve pas de solution.
Merci par avance. :help:
Petit problème sur une récapitulation de dérivation
3 messages
- Page 1 sur 1
Salut !
C'est parce qu'à tous les coups, tu as développer l'expression de) , puis dérivé termes à termes.
, puis dérivé termes à termes.
En voyant plutôt comme un produit de fonctions
comme un produit de fonctions  où
où =(x-1)^2) et
et =(x+2)^2) , on a
, on a =u'(x)v(x) + u(x)v'(x) =...) :+++:
:+++:
Sachant calculer les dérivées de et
et  , on peut d'ores et déjà savoir que
, on peut d'ores et déjà savoir que =(x-1)(x+2)(...)) :++:
:++:
Sinon, si tu veux continuer ton raisonnement, on a l'identité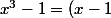(x^2+x+1)) :+++:
:+++:
C'est parce qu'à tous les coups, tu as développer l'expression de
En voyant plutôt
Sachant calculer les dérivées de
Sinon, si tu veux continuer ton raisonnement, on a l'identité
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Merci pour ta réponse.
En fait j'ai appliqué la théorie donnée en classe pour la dérivée sans développer l'expression de f(x). J'ai effectué ainsi:
h': (x-1)^2 = 2(x-1) (1)
i': (x+2)^2 = 2(x+2) (1)
les (1) étant évidemment optionnels: c'est simplement pour démontrer que j'ai suivi la théorie. Puis:
f' = 2(x-1) (1) (x+2)^2 + 2(x+2) (1) (x-1)^2
Donc si je t'ai bien suivi j'ai effectivement appliqué la solution que tu as donnée dans ta 2ème ligne.
Mais là où tu diffères, si je te comprends bien, c'est que tu pars de cette base pour faire ta mise en évidence et ton regroupement sans développer, ce qui donne:
2(x-1) (x+2) (x+2+x-1) = 2(x-1) (x+2) (2x+1)
-> 2(x-1) (x+2) (2x+1) = 0
et là je peux trouver les zéros sur cette base. MERCI à toi. :+++:
Tu es un chef.
Ma dérivée est correcte, mais comme nous n'utilisions pas de (x^3 - 1) et que nous allions jusqu'au bout de la dérivée pour appliquer le regroupement et la mise en évidence, ce n'était pas gagné.
En fait j'ai appliqué la théorie donnée en classe pour la dérivée sans développer l'expression de f(x). J'ai effectué ainsi:
h': (x-1)^2 = 2(x-1) (1)
i': (x+2)^2 = 2(x+2) (1)
les (1) étant évidemment optionnels: c'est simplement pour démontrer que j'ai suivi la théorie. Puis:
f' = 2(x-1) (1) (x+2)^2 + 2(x+2) (1) (x-1)^2
Donc si je t'ai bien suivi j'ai effectivement appliqué la solution que tu as donnée dans ta 2ème ligne.
Mais là où tu diffères, si je te comprends bien, c'est que tu pars de cette base pour faire ta mise en évidence et ton regroupement sans développer, ce qui donne:
2(x-1) (x+2) (x+2+x-1) = 2(x-1) (x+2) (2x+1)
-> 2(x-1) (x+2) (2x+1) = 0
et là je peux trouver les zéros sur cette base. MERCI à toi. :+++:
Tu es un chef.
Ma dérivée est correcte, mais comme nous n'utilisions pas de (x^3 - 1) et que nous allions jusqu'au bout de la dérivée pour appliquer le regroupement et la mise en évidence, ce n'était pas gagné.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
