Salut,
je dois calculer l'intégrale de (1-cos(x))/x² entre - infini et +infini. Je sais que le résultat est Pi mais j'aimerais avoir la démonstration.
Merci d'avance!
Intégrale à calculer
10 messages
- Page 1 sur 1
kubrick73 a écrit:Salut,
je dois calculer l'intégrale de (1-cos(x))/x² entre - infini et +infini. Je sais que le résultat est Pi mais j'aimerais avoir la démonstration.
Merci d'avance!
Par un argument de parité relatif à la fonction
Ensuite, tu remarqueras surement qu'on risque d'avoir des problèmes en 0 et +\infty pour calculer
- A l'aide d'un DL, montre que
- Sachant que
Pour trouver une primitive de
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Bonsoir, est-ce que ça aurait un intérêt de passer le cosinus en série entière et d'intervertir les signes somme et intégrale ?
Il faudrait écrire ça comment ?
D'abord étudier la série entière et sa convergence ?
Et poser = \int_0^x f(t) \cdot dt) ...
...
J'ai l'impression que ça ne marche pas ou alors que ce serait trop tordu comme il faut repasser à la limite...
Quelqu'un peut au passage m'éclairer sur ça ?
Surtout j'imagine que ça aurait un intérêt ici seulement si on arrive à "utiliser la série intégrée"... pour trouver la valeur... de l'intégrale de départ.
Il faudrait écrire ça comment ?
D'abord étudier la série entière et sa convergence ?
Et poser
J'ai l'impression que ça ne marche pas ou alors que ce serait trop tordu comme il faut repasser à la limite...
Quelqu'un peut au passage m'éclairer sur ça ?
Surtout j'imagine que ça aurait un intérêt ici seulement si on arrive à "utiliser la série intégrée"... pour trouver la valeur... de l'intégrale de départ.
capitaine nuggets a écrit:Par un argument de parité relatif à la fonction, montre que calculer ton intégrale revient seulement à calculer
et qu'en fait
.
Ensuite, tu remarqueras surement qu'on risque d'avoir des problèmes en 0 et +\infty pour calculer.
- A l'aide d'un DL, montre queexiste et est finie ;
- Sachant queest bornée, montre que
existe et est finie.
Pour trouver une primitive de, il faut effectuer deux intégrations par parties visant à finir avec une intégrale contenant seulement
:+++:
Ok merci, mais pour la double IPP, c'est peut être évident mais je vois pas comment faire disparaitre le 1/x^2..
Salut,
Je ne pense pas qu'on puisse obtenir facilement la valeur de cette intégrale.
Par contre, un truc archi classique dans ce genre de cas, c'est d'introduire un terme supplémentaire pour évacuer la division par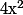 :
:
}{x^2}dx=2F(0)\) où, pour tout
où, pour tout =\int_{0}^{+\infty}\frac{1-\cos(x)}{x^2} e^{-tx}\,dx)
On vérifie que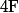 est continue sur
est continue sur  , dérivable sur
, dérivable sur  et que
et que =-\int_{0}^{+\infty}\frac{1-\cos(x)}{x} e^{-tx}dx)
Qui est de nouveau dérivable sur avec
avec =\int_{0}^{+\infty}\big(1-\cos(x)\big)e^{-tx}dx=\frac{1}{t}-\frac{t}{t^2+1})
Donc=\ln(t)-\frac{1}{2}\ln(1+t^2)+Cst) avec
avec  car
car \longrightarrow_{t\to\infty}0)
D'où=-\frac{1}{2}t\ln\Big(1+\frac{1}{t^2}\Big)-\arctan(t)+Cst) avec
avec  car
car \longrightarrow_{t\to\infty}0)
et on en déduit que=\frac{\pi}{2}) .
.
Je ne pense pas qu'on puisse obtenir facilement la valeur de cette intégrale.
Par contre, un truc archi classique dans ce genre de cas, c'est d'introduire un terme supplémentaire pour évacuer la division par
On vérifie que
Qui est de nouveau dérivable sur
Donc
D'où
et on en déduit que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Salut,
Je ne pense pas qu'on puisse obtenir facilement la valeur de cette intégrale.
Par contre, un truc archi classique dans ce genre de cas, c'est d'introduire un terme supplémentaire pour évacuer la division par:
où, pour tout
On vérifie queest continue sur
, dérivable sur
et que
Qui est de nouveau dérivable suravec
Doncavec
car
D'oùavec
car
et on en déduit que.
Super méthode ça...
Par contre, comment on justifie correctement que F(t) tend vers 0 ?
Faut majorer l'exponentielle ? Mais je ne vois pas comment vu que le x "commence" en 0.
En fait, contrairement a ce que j'ai fait... :hum:, il faut tout justifier bien proprement....BiancoAngelo a écrit:Par contre, comment on justifie correctement que F(t) tend vers 0 ?
Faut majorer l'exponentielle ? Mais je ne vois pas comment vu que le x "commence" en 0.
Le fait que F et F' tendent vers 0 lorsque t->oo n'est pas bien dur a démontrer vu que dans les deux cas, la fonction avant le exp(-tx) se prolonge parfaitement en x=0 et tend vers 0 lorsque x->+oo donc, elle est bornée sur R+ par un certain M (évidement indépendant de t) et on peut majorer (en valeur absolue) l'intégrale par
Sinon, il y a sans doute d'autres méthodes (par exemple avec les résidus sur C, peut-être aussi avec des transformées de Fourrier ou de Laplace), mais je ne pense pas qu'on puisse l'obtenir "simplement", c'est à dire uniquement avec des changement de variables et des I.p.P.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
