Matrices et fonction

[capitaine nuggets]

Okay c'est bon je trouvais pas comme toi mais je mettais trompé, je trouve pareil.

Maintenant faut que je trouve les valeurs propres de Hf en P(-3, -4, -3).



Comment on modifie Hf pour qu'il soit en P?

Les valeurs propres sont racines du polynôme caractéristique

[Manaus]

Les valeurs propres sont racines du polynôme caractéristique

Donc en fait si dans Hf je n'ai pas d'inconnu, je n'ai pas besoin de déterminer les points critiques?? :doh:

[capitaine nuggets]

Donc en fait si dans Hf je n'ai pas d'inconnu, je n'ai pas besoin de déterminer les points critiques?? :doh:

Je ne comprends pas bien ta question...
Normalement il faut le faire avec appliquée au point voulue sauf que là les dérivées partielles rendent toutes les fonctions dans constantes :we:

[Manaus]

Je ne comprends pas bien ta question...
Normalement il faut le faire avec appliquée au point voulue sauf que là les dérivées partielles rendent toutes les fonctions dans constantes :we:

Ce qui fait que dans ce cas là j'aurai pu éviter de calculer les points critiques?

[capitaine nuggets]

Ce qui fait que dans ce cas là j'aurai pu éviter de calculer les points critiques?

Pourquoi dis-tu cela ?

On a un point critique : (-3,-4,-3).
Suivant le signe des valeurs propres de la matrice hessienne en ce point, on pourra juger si (-3,-4,-3) est un maximum local, minimum local ou un point-selle.

Chaque élément de est de la forme où désigne deux variables parmi .

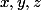
Pris au point (-3,-4,-3), ces éléments sont l'image par la fonction de ce triplet : .
Là il se trouve que les dérivées partielles rendent toutes les fonctions constantes. Or l'image par une fonction constante de (-3,-4,-3) étant cette même constante, il n'y a rien à calculer.
Il faut donc trouver les valeurs propres de .

[Manaus]

J'essaye de trouver les valeurs propres mais j'arrive pas non plus :/ je suis vraiment nul la dedans je suis désolé... Mais en tout cas merci car tu m'aide vraiment à tout comprendre!

[capitaine nuggets]

Ne t'en fais pas, ce n'est pas trop compliqué :+++:

Les valeurs propres sont racines du polynôme caractéristique

Les valeurs propres sont donc solutions de l'équation .
Calcule donc .

[Manaus]

Que dois je mettre pour le lambda?

[capitaine nuggets]

Que dois je mettre pour le lambda?

Rien : c'est l'inconnue dans l'équation.

[Manaus]

Ah oui c'est vrai... Mais comment le sortir du dét alors pour pouvoir le calculer?

[capitaine nuggets]

Le sortir du déterminant ???

Il s'agit juste de calculer un déterminant d'une matrice :+++:

Si alors on a .

Donc les valeurs propres sont solutions de l'équation , c'est-à-dire, .

[Manaus]

Le sortir du déterminant ???

Il s'agit juste de calculer un déterminant d'une matrice :+++:

Si alors on a .

Donc les valeurs propres sont solutions de l'équation , c'est-à-dire, .

Ah mais ouiiiii... Je fatigue je crois!! C'est tout bon la, merci beaucoup pour ton aide, tes explications qui m'ont permit de bien comprendre et ta patience :lol3:

[capitaine nuggets]

Ah mais ouiiiii... Je fatigue je crois!! C'est tout bon la, merci beaucoup pour ton aide, tes explications qui m'ont permit de bien comprendre et ta patience :lol3:

Pas de soucis, je sais que ce ne sont pas des choses forcément triviales au début :+++:

[capitaine nuggets]

Je te laisse deux ou trois réponses pour te permettre de contrôler tes résultats :
(si je ne me suis pas trompé)

-

- Le spectre (ou l'ensemble des valeurs propres de ) est .

- admet un maximum local en et

[Manaus]

Merci beaucoup pour ta gentillesse!! Je finirai mes calculs demain y'a pas de raison que je ne trouve pas la même chose que toi maintenant :)