Bonjour à tous,
Il y a une question que je n'arrive pas à résoudre dans mon DM de maths (et ce n'est pas faute d'avoir cherché :triste: ).
La voici :
"Soit ABC un triangle isocèle en A, avec A=36 degrés.
La bissectrice issue de C coupe [AB] en D.
Exprimer la longueur BD en fonction de cos(72) de deux façons (on peut se placer dans le triangle BCD d'une part, et ABC d'autre part."
La première est simple, on se place dans le triangle BCD, et en utilisant la hauteur issue de C, on trouve que BD=2*cos(72)*BC.
Mon problème est que je n'arrive pas à trouver la 2ème façon ( peut-être une propriété sur la bissectrice que je n'ai pas vue?).
(Au cas où cela pourrait aider, la question suivante est : " en déduire que cos(72) est solution de l'équation 4x² + 2x - 1 = 0.")
En tout cas, merci d'avance pour votre aide.
Kaki
DM Maths
13 messages
- Page 1 sur 1
Salut,
Il y a des tas de façons d'obtenir des relations concernant les longueurs/angles de ton dessin.
Il y a évidement toutes celles utilisé par mathelot dans son pdf (qui suffisent à tout déterminer), mais on peut aussi
- Utiliser la loi des cosinus (appelée "formule d'Al-Kashi" dans le système scolaire français) dans le triangle BCD
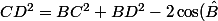BC\,BD) qui, compte tenu du fait que BC=CD donne
qui, compte tenu du fait que BC=CD donne 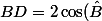BC)
- Utiliser le fait (je suis pas sûr que ce soit vu au Lycée) que, dans un triangle ABC quelconque, la bissectrice intérieure issue de C coupe (AB) en) donc
donc 
- Utiliser le fait que les triangles BCD et CAB sont semblables donc
...etc...
Il y a des tas de façons d'obtenir des relations concernant les longueurs/angles de ton dessin.
Il y a évidement toutes celles utilisé par mathelot dans son pdf (qui suffisent à tout déterminer), mais on peut aussi
- Utiliser la loi des cosinus (appelée "formule d'Al-Kashi" dans le système scolaire français) dans le triangle BCD
- Utiliser le fait (je suis pas sûr que ce soit vu au Lycée) que, dans un triangle ABC quelconque, la bissectrice intérieure issue de C coupe (AB) en
- Utiliser le fait que les triangles BCD et CAB sont semblables donc
...etc...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
