Terminale S - raisonner par récurrence

[whatever]

....................

[mathelot]

bonjour,

j'espère (pour toi) que ta formule est exacte.

pour la démontrer par récurrence , il y a une difficulté

non seulement la somme augmente d'un terme en passant de n à n+1
mais le facteur (n-k) change en (n+1-k)

comment vas tu faire ?

[whatever]

bonjour,

j'espère (pour toi) que ta formule est exacte.

pour la démontrer par récurrence , il y a une difficulté

non seulement la somme augmente d'un terme en passant de n à n+1
maiss le facteur (n-k) change en (n+1-k)

comment vas tu faire ?

Peut-être fallait il que je conjecture la formule Sn+1 puis que je cherche à trouver Sn en raisonnant par récurrence ?

[mathelot]

Bien joué! ta conjecture est exacte.

il ne reste plus qu'à poser l'hypothèse de récurrence.

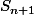
Ensuite , essaye de développer qui:

- comprend un terme de plus

- possède le facteur

il y a p-e besoin de la formle de cours

[whatever]

je dois trouver Sn+1 à partir de la formule que j'ai trouvé pour Sn ?

[whatever]

ou bien je dois partir de la formule de l'énoncé et ensuite démontrer Sn+1 que j'aurai trouvé par récurrence ?

[mathelot]

On démarre avec

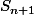
et sa définition.

En cours de calcul , apparait dans l'écriture de

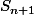
On remplace alors par la formule posée en hypothèse de récurrence

pour essayer de la retrouver au rang (n+1)

[whatever]

........................

[mathelot]

L' hypothèse de récurrence est exacte, j'ai calculé directement

la formule que tu proposais par les polynomes de Bernoulli. Elle est exacte.

Il faudrait essayer de distribuer le facteur k sur l'autre facteur (n+1-k)=(n-k)+1

De plus, la somme, au rang (n+1), possède un terme de plus (on somme jusqu' à (n+1))

[mathelot]

...................

[mathelot]

tu as noté la démonstration de la récurrence, que j'efface....?

[whatever]

non je n'ai pas noté

[Sa Majesté]

On n'efface pas les messages, c'est une raison de bannissement définitif du forum.
Merci de signaler à la modération tout message effacé.