Boujours à tous, j'aurais besoin de votre aide car je dois faire un DM et je ne comprends pas grand chose voir rien du tout. :help:
Voici mon énnoncé :
1. a) déterminer un polynôme P, de degré 2, verifiant pour tout x : P(x+1)-P(x)=x
b) prouvez l'egalité : 1+2+...+n=P(n+1)-P(1)
c) en deduire la formule : 1+2...+n=n(n+1)/2
Merci d'avance et désolé pour les fautes d'orthographe :3
Second degré polynôme 1èreS
7 messages
- Page 1 sur 1
Bruzy a écrit:Boujours à tous, j'aurais besoin de votre aide car je dois faire un DM et je ne comprends pas grand chose voir rien du tout. :help:
Voici mon énnoncé :
1. a) déterminer un polynôme P, de degré 2, verifiant pour tout x : P(x+1)-P(x)=x
b) prouvez l'egalité : 1+2+...+n=P(n+1)-P(1)
c) en deduire la formule : 1+2...+n=n(n+1)/2
Merci d'avance et désolé pour les fautes d'orthographe :3
Bonsoir,
j'ai tout simplement développé, à savoir :
Px + P -Px = x
P =x
Vérif : si P=x alors x(x+1)-x.x = x²+x-x² = x c'est bien cela à ceci prés que P obtenu n'est pas de degré 2 ! Si quelqu'un peut nous aider, ça serait avec plaisir ! merci d'avance
polynomes de Bernoulli
i.a) un polynôme de degré 2 est
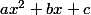
La condition s'écrit
-P(x)=a(x^2+2x+1)+b(x+1)+c -(ax^2+bx+c)=x)
on réduit, on identifie les coefficients pour trouver a et b (on prend c=0, on est intéressé à l'existence
du polynôme, pas à son unicité).
i.b)
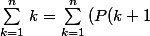-P(k)))
l'intérêt de la méthode c'est qu'elle se généralise. Comment ?
La condition s'écrit
on réduit, on identifie les coefficients pour trouver a et b (on prend c=0, on est intéressé à l'existence
du polynôme, pas à son unicité).
i.b)
l'intérêt de la méthode c'est qu'elle se généralise. Comment ?
mathelot a écrit:i.a) un polynôme de degré 2 est
La condition s'écrit
on réduit, on identifie les coefficients pour trouver a et b (on prend c=0, on est intéressé à l'existence
du polynôme, pas à son unicité).
i.b)
l'intérêt de la méthode c'est qu'elle se généralise. Comment ?
Merci bcp.
J'ai compris concernant la question 1.a) mais pas la b)
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
