Courbe de densité
13 messages
- Page 1 sur 1
Courbe de densité
Bonjour,
Quel qu'un peut il m'indiquer la marche à suivre pour créer une courbe de densité, à partir d' un histogramme...et de là comment retrouve t on l'équation de cette courbe.
Je suis en DAEU, et nous devons faire un "mini mémoire", bon ce n'est pas le bon terme, mais au moins vous me comprendrez, et je suis à cette étape et je ne sais pas comment faire...
En DAEU on survole les choses et ça j'ai dû mal avec ça...merci pour vos réponses,
Par contre mon analyse est d'ordre statistique et non probabiliste, est ce que ça pose problème?
Et mes données pour cette partie ne sont pas discrètes elles sont continues.
Merci d'avance.
Quel qu'un peut il m'indiquer la marche à suivre pour créer une courbe de densité, à partir d' un histogramme...et de là comment retrouve t on l'équation de cette courbe.
Je suis en DAEU, et nous devons faire un "mini mémoire", bon ce n'est pas le bon terme, mais au moins vous me comprendrez, et je suis à cette étape et je ne sais pas comment faire...
En DAEU on survole les choses et ça j'ai dû mal avec ça...merci pour vos réponses,
Par contre mon analyse est d'ordre statistique et non probabiliste, est ce que ça pose problème?
Et mes données pour cette partie ne sont pas discrètes elles sont continues.
Merci d'avance.
Si les rectangles qui constituent ton histogramme on tous la même largeur, les sommets de tes rectangles définissent une fonction constante sur chaque classe et leur ensemble une fonction étagée qui est une densité f de probabilité. on a bien f>=0 et  dt) =
= =1. si su veux passer en continu, tu peux prendre
=1. si su veux passer en continu, tu peux prendre  dt) ; tu auras alors une fonction continue et affine par morceau, mais sera la fonction répartition de la densité définie naturellement par ton histogramme (intéressant); sinon,ça me paraît être un problème très difficile; on peut obtenir la fameuse courbe de Gauss à partir de la loi binomiale B((2n,1/2) centrée réduite en faisant tendre n vers +oo, mais c'est de la haute voltige! De toute façon, si on pouvait extraire de chaque histogramme une densité continue, ça se saurait!
; tu auras alors une fonction continue et affine par morceau, mais sera la fonction répartition de la densité définie naturellement par ton histogramme (intéressant); sinon,ça me paraît être un problème très difficile; on peut obtenir la fameuse courbe de Gauss à partir de la loi binomiale B((2n,1/2) centrée réduite en faisant tendre n vers +oo, mais c'est de la haute voltige! De toute façon, si on pouvait extraire de chaque histogramme une densité continue, ça se saurait!
bon courage.
bon courage.
Merci Paquito pour ta réponse et tes encouragements...
Concernant ton explication,je crois l'avoir comprise mais dans le concret je ne sais pas trop en faite...
je ne sais si je vais tenter de le faire à partir de donnée continue, car la haute voltige c'est pas trop mon truc...enfin je ne sais pas je vais voir....
Par contre un prof m' a expliqué plus ou moins la marche à suivre concernant des données dites discrètes mais il y a des choses sur lesquelles je bute :
D'abord explication de mon sujet je fais une analyse des élèves DAEU et j'ai eu le droit d'avoir la liste des élèves ayant validé entre 0 et 4 matières (il faut 4 matières pour valider le DAEU)
D'abord mon analyse et mon problème commence par les filles (154 filles en tout)
Après dépouillement j'obtiens cela
46 filles qui ont validé 0 matière (en pourcentage 29.87% arrondie à 30%) point A (0,30)
32 filles qui ont validé 1 matière (en pourcentage 20.77% arrondie à21%) point B (1,21)
31 filles qui ont validé 2 matières (en pourcentage 20.12% arrondie à 20%) point C (2, 20)
31 filles qui ont validé 3 matières (en pourcentage 20.12%, arrondie à20%) point D (3,20)
14 filles qui ont validé 4 matières (en pourcentage 9.09%, arrondie à 9%) point E (4,9)
Sur Géogébra je place mes points (A,B,C,D,E) et je cherche la fonction polynôme correspondante à ces points et j'obtiens F(x) = -0.2x^4 + 0.1x^3 + 5.2x² -14.1x +30
Ensuite on cherche le point d'intersection entre la courbe et l'axe des abscisses et j'ai 2 points F, et G, mais ici seul G est pertinent (4.3 , 0)
Ensuite toujours par le biais de Géogébra je calcule intégrale de f(x) entre 0 et x(G)
j'obtiens 82.72 ua (noté nombre a sur Géogébra)
Après je trace la fonction d(x) (fonction densité) = f(x)/ a,
Après je calcule l'intégrale de d(x) entre 0 et 4 et j'obtiens bien 1,
Par contre je dois retrouver mes valeurs de début :
Maintenant, je vais retrouver les valeurs de mon tableau à laide du calcul dintégrale de d(x) sur Géogébra :
Entre [0,1[ :
je calcule l'intégrale d(x) entre 0 et 1 je retrouve 0.3, donc 0.3*100= 30% donc je retrouve le pourcentage de fille qui ont 0 matière
Entre [1,2[ :
je calcule l'intégrale d(x) entre 1 et 2 je retrouve 0.2, donc 0.2*100= 20%, bon normalement je devrais retrouver 21% Mais bon je me dis ça passe , erreur d'arrondie?
Entre [2,3[
je calcule l'intégrale d(x) entre 2 et 3 je retrouve 0.2, donc 0.2*100= 20%, donc là je retrouve le nombre de filles qui ont validé une matière
entre [3,4[
je calcule l'intégrale d(x) entre 3 et 4 et je on retrouve 0.2, donc 0.2*100= 20%, donc là je retrouve le nombre de filles qui ont validé 3 matières
Après je ne sais comment faire pour retrouver les personnes qui ont validé 4 matières....
je vais mettre les différents graphes obtenus sur Geogébra en dessous
Concernant ton explication,je crois l'avoir comprise mais dans le concret je ne sais pas trop en faite...
je ne sais si je vais tenter de le faire à partir de donnée continue, car la haute voltige c'est pas trop mon truc...enfin je ne sais pas je vais voir....
Par contre un prof m' a expliqué plus ou moins la marche à suivre concernant des données dites discrètes mais il y a des choses sur lesquelles je bute :
D'abord explication de mon sujet je fais une analyse des élèves DAEU et j'ai eu le droit d'avoir la liste des élèves ayant validé entre 0 et 4 matières (il faut 4 matières pour valider le DAEU)
D'abord mon analyse et mon problème commence par les filles (154 filles en tout)
Après dépouillement j'obtiens cela
46 filles qui ont validé 0 matière (en pourcentage 29.87% arrondie à 30%) point A (0,30)
32 filles qui ont validé 1 matière (en pourcentage 20.77% arrondie à21%) point B (1,21)
31 filles qui ont validé 2 matières (en pourcentage 20.12% arrondie à 20%) point C (2, 20)
31 filles qui ont validé 3 matières (en pourcentage 20.12%, arrondie à20%) point D (3,20)
14 filles qui ont validé 4 matières (en pourcentage 9.09%, arrondie à 9%) point E (4,9)
Sur Géogébra je place mes points (A,B,C,D,E) et je cherche la fonction polynôme correspondante à ces points et j'obtiens F(x) = -0.2x^4 + 0.1x^3 + 5.2x² -14.1x +30
Ensuite on cherche le point d'intersection entre la courbe et l'axe des abscisses et j'ai 2 points F, et G, mais ici seul G est pertinent (4.3 , 0)
Ensuite toujours par le biais de Géogébra je calcule intégrale de f(x) entre 0 et x(G)
j'obtiens 82.72 ua (noté nombre a sur Géogébra)
Après je trace la fonction d(x) (fonction densité) = f(x)/ a,
Après je calcule l'intégrale de d(x) entre 0 et 4 et j'obtiens bien 1,
Par contre je dois retrouver mes valeurs de début :
Maintenant, je vais retrouver les valeurs de mon tableau à laide du calcul dintégrale de d(x) sur Géogébra :
Entre [0,1[ :
je calcule l'intégrale d(x) entre 0 et 1 je retrouve 0.3, donc 0.3*100= 30% donc je retrouve le pourcentage de fille qui ont 0 matière
Entre [1,2[ :
je calcule l'intégrale d(x) entre 1 et 2 je retrouve 0.2, donc 0.2*100= 20%, bon normalement je devrais retrouver 21% Mais bon je me dis ça passe , erreur d'arrondie?
Entre [2,3[
je calcule l'intégrale d(x) entre 2 et 3 je retrouve 0.2, donc 0.2*100= 20%, donc là je retrouve le nombre de filles qui ont validé une matière
entre [3,4[
je calcule l'intégrale d(x) entre 3 et 4 et je on retrouve 0.2, donc 0.2*100= 20%, donc là je retrouve le nombre de filles qui ont validé 3 matières
Après je ne sais comment faire pour retrouver les personnes qui ont validé 4 matières....
je vais mettre les différents graphes obtenus sur Geogébra en dessous
Finalement, c'est un diagramme en bâtons avec 5 valeurs consécutives que tu as; je suis très surpris que tu veuilles passer à une densité liée à une variable continue; je ne vois pas du tout l'intérêt.
Tel que tu t'y prends, tu est obligé de trouver une densité qui est associée à une v.a.qui est censée prendre toutes les valeurs de [0; x(G)], mais avec une densité continue P(0=
Tel que tu t'y prends, tu est obligé de trouver une densité qui est associée à une v.a.qui est censée prendre toutes les valeurs de [0; x(G)], mais avec une densité continue P(0=
Tu as déjà de la chance que ça marche à peu prés pour les autres.
Bonjour Paquito,
le but du jeu est en fait de montrer que l'on est capable d'utiliser les notions appris en math10 (niveau de DAEU) dans un exercice quelconque même si cela ne nous apporte rien en fait....ici mon but est de modéliser sous forme d'une courbe de densité les données recueillis en premier lieu.
Un autre exemple le semestre j' avais comparé le trajet entre 2 ports en calculant avec la méthode des douzièmes et je l'avais comparé à un calcul de marée avec la méthode des moindres carrés (notion appris alors en math9)...il faut savoir réutiliser les notions apprises...
Pour le reste je n'ai pas compris...je me demande si j'ai bien compris ce que le prof a expliqué..;pourquoi tu dis que j'ai de la chance...ce n'est pas normal que cela fonctionne au début?
le but du jeu est en fait de montrer que l'on est capable d'utiliser les notions appris en math10 (niveau de DAEU) dans un exercice quelconque même si cela ne nous apporte rien en fait....ici mon but est de modéliser sous forme d'une courbe de densité les données recueillis en premier lieu.
Un autre exemple le semestre j' avais comparé le trajet entre 2 ports en calculant avec la méthode des douzièmes et je l'avais comparé à un calcul de marée avec la méthode des moindres carrés (notion appris alors en math9)...il faut savoir réutiliser les notions apprises...
Pour le reste je n'ai pas compris...je me demande si j'ai bien compris ce que le prof a expliqué..;pourquoi tu dis que j'ai de la chance...ce n'est pas normal que cela fonctionne au début?
Pour moi, puisque tu as des valeurs entière consécutives, une première étape serait de passer à un histogramme, en prenant pour bases [-0,5; 0,5] pour 0, ...,jusqu'à [3,5;4,5] pour 4; et en prenant pour hauteur les fréquences: 0,3 pour 0; 0,2 pour 1; etc.... l'aire de chaque rectangle est donc égal à la probabilité de la valeur et c'est en fait l'intégrale d'une fonction constante;
f(x)= 0,3 sur [-0,5; 0,5] et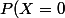=\bigint_{-0,5}^{0,5}f(x)dx=0,3) . Ensuite pourquoi ne pas appliquer ta méthode, mais en travaillant sur [-0,5; 4,4]; évidemment ton idée de prendre l'unique polynôme de degré 4 qui passe par tes 5 points est excellente.
. Ensuite pourquoi ne pas appliquer ta méthode, mais en travaillant sur [-0,5; 4,4]; évidemment ton idée de prendre l'unique polynôme de degré 4 qui passe par tes 5 points est excellente.
J'obtiensdx=103,5) , donc d(x) devient p(x)/103,5, puis les calculs donnent:
, donc d(x) devient p(x)/103,5, puis les calculs donnent: 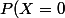=\bigint_{-0,5}^{0,5}d(x)dx=0,294) ,
,=\bigint_{0,5}^{1,5}d(x)dx=0,206) ,
, 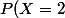=\bigint_{1,5}^{2,5}d(x)dx=0,196) ,
,
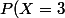=\bigint_{2,5}^{3,5}d(x)dx=0,199) et
et 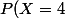=\bigint_{-3,5}^{4,4}d(x)dx=0,106) .
.
Non seulement la démarche me semble beaucoup plus logique, mais en plus les résultats sont satisfaisants.
N'oublie pas de poser d(x)=0 pour x4,4 car une densité doit vérifier:dx=1.)
f(x)= 0,3 sur [-0,5; 0,5] et
J'obtiens
Non seulement la démarche me semble beaucoup plus logique, mais en plus les résultats sont satisfaisants.
N'oublie pas de poser d(x)=0 pour x4,4 car une densité doit vérifier:
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :




