Résoudre les différentielles suivanttes

[HERCOLUBUS]

Salut à tous,

Je dois résoudre les différentielles suivantes en tenant compte de la condition initiale:

et

et

J'aimerais savoir comment les résoudre...


Merci !

[capitaine nuggets]

Salut !

Salut à tous,

Je dois résoudre les différentielles suivantes en tenant compte de la condition initiale:

et

et

J'aimerais savoir comment les résoudre...


Merci !

Rassemble les termes en "y" d'un côté et "x" de l'autre :

Par suite, on a :

[capitaine nuggets]

Salut à tous,

Je dois résoudre les différentielles suivantes en tenant compte de la condition initiale:

et

et

J'aimerais savoir comment les résoudre...


Merci !

La seconde, 'faut faire plus attention.
Des solutions existent si et seulement si , c'est-à-dire, si et son image par sont de même signes !
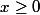
Traitons le premier cas : supposons et .
Alors, en regroupant de part et d'autres termes en "x" et termes en "y", il vient :



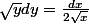
Primitive ensuite des deux côtés !

[HERCOLUBUS]

Salut !



Rassemble les termes en "y" d'un côté et "x" de l'autre :

Par suite, on a :

J'arrive à mais le corrigé indique

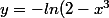[capitaine nuggets]

J'arrive à mais le corrigé indique

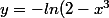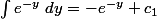
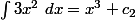
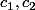
et avec deux contantes réelles.
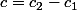
Ainsi, en posant , on a -e^{-y} = x^3+c c'est-à-dire e^{-y}= - x^3 - c.
Ensuite, on passe au Ln (le Ln n'est définie que sur !)
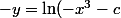Dans le cas, où , c'est-à-dire ... , on a avec .
En utilisant la condition initiale, on trouve bien pour ,.