Résolution problème
17 messages
- Page 1 sur 1
résolution problème
Bonjour,
Je n'arrive pas à déterminer cela:
1. trouvez l'ensemble des solutions de l'inéquation suivante avec x>0:
(-x^3a + 2x^a - 1) / (1 - x^3a )
on m'indique que l'on pose x^a=x
je trouve S= ] (1+rac(5))/2 ; (1-rac(5)/2) [
Puis, on me demande de trouvez la plus petite valeur de a pour laquelle le nombre 49/51 appartient à J
==> je ne sais pas comment faire.
Merci de me dire comment avancer dans mon problème.
Je n'arrive pas à déterminer cela:
1. trouvez l'ensemble des solutions de l'inéquation suivante avec x>0:
(-x^3a + 2x^a - 1) / (1 - x^3a )
on m'indique que l'on pose x^a=x
je trouve S= ] (1+rac(5))/2 ; (1-rac(5)/2) [
Puis, on me demande de trouvez la plus petite valeur de a pour laquelle le nombre 49/51 appartient à J
==> je ne sais pas comment faire.
Merci de me dire comment avancer dans mon problème.
Désolé je me suis trompée et puis j'ai réussi à trouver.
Par contre j'aurai besoin d'aide pour ces questions:
soit E un ensemble de suites u réelles:
on a : E : pu(n+2)-u(n+1)+(1-p)u(n+2)
on veut montrer que pour p = 1/2 E est arithmétique
ensuite, pour p différent de 1/2 je,dois trouver le terme génral de u(n)
mais je ne vois pas comment l'écrire
Merci pour toute aide apportée
Par contre j'aurai besoin d'aide pour ces questions:
soit E un ensemble de suites u réelles:
on a : E : pu(n+2)-u(n+1)+(1-p)u(n+2)
on veut montrer que pour p = 1/2 E est arithmétique
ensuite, pour p différent de 1/2 je,dois trouver le terme génral de u(n)
mais je ne vois pas comment l'écrire
Merci pour toute aide apportée
bentaarito a écrit:Encore une fois un énoncé erronné..
le p se simplifie tel que tu l'as écrit donc je vois pas l'origine de ta question
Je vous écris l'énoncé ;
soit p un réel tel que 01
on désigne E l'ensemble des suites u réelles qui satisfont cela:
pu(n+2) - u(n+1) + (1-p)u(n) = 0
si p=1/2 montrer que E est arithmétique
si p différent de 1/2 écrire alors l'expression générale de u(n) d'une suite u quelconque de E
En espérant que ce soit plus clair...
C'est une relation de récurrence linéaire d'ordre 2, vous avez du faire un cours là dessus.
C'est à dire
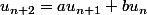
On cherche les solutions de type géométrique c'est à dire on détermine q , non nul, tel que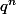 soit solution.
soit solution.
En remplaçant puis en divisant par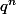 on trouve que c'est équivalent à q solution de q² = aq + b
on trouve que c'est équivalent à q solution de q² = aq + b
Si cette équation admet deux solutions réelles distinctes (c'est le cas, ici, lorsque p est différent de 0.5)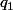 et
et 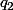 , alors la solution générale est du type :
, alors la solution générale est du type :
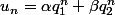
C'est à dire
On cherche les solutions de type géométrique c'est à dire on détermine q , non nul, tel que
En remplaçant puis en divisant par
Si cette équation admet deux solutions réelles distinctes (c'est le cas, ici, lorsque p est différent de 0.5)
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
