Votre aide est importante pour la suite de mon DM
Je dois determiner le maximum / minimum de 2xau carré - 4x -2 et préciser les coordonnées de S
Merci d'avance !!!
Urgent
7 messages
- Page 1 sur 1
Salut,
Calculer la dérivée permet de voir les variations de la fonction, je note f ta fonction.
=4x-4)
On résout
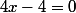

Cela veut dire qu'il y a un changement de monotonie (croissant-décroissant ou l'inverse) en x = 1. On voit que pour x 1, f'(x) est positif.
Le changement se fait donc : décroissant puis croissant. Entre les deux (c.a.d. quand x = 1) on trouve donc le minimum que peut prendre la valeur f(x).
Pour connaitre cette valeur on cherche la coordonnées y qui correspond à x = 1 sur la courbe f. Autrement dit on calcule f(1)=...=-4
Il n'y a visiblement pas de maximum, on pourrait calculer la limite en -infini ou +infini de f(x) pour s'en convaincre.
Qu'est-ce que S ?
Calculer la dérivée permet de voir les variations de la fonction, je note f ta fonction.
On résout
Cela veut dire qu'il y a un changement de monotonie (croissant-décroissant ou l'inverse) en x = 1. On voit que pour x 1, f'(x) est positif.
Le changement se fait donc : décroissant puis croissant. Entre les deux (c.a.d. quand x = 1) on trouve donc le minimum que peut prendre la valeur f(x).
Pour connaitre cette valeur on cherche la coordonnées y qui correspond à x = 1 sur la courbe f. Autrement dit on calcule f(1)=...=-4
Il n'y a visiblement pas de maximum, on pourrait calculer la limite en -infini ou +infini de f(x) pour s'en convaincre.
Qu'est-ce que S ?
Non pour trouver le minimum de f(x) il faut calculer f(1) pas f'(1).
On cherchait pour quelle valeur de x, f'(x) = 0 on a trouvé 1 donc f'(1) = 0 c'est déjà fait.
Au fait vérifie dans l'énoncé que la fonction est définie sur IR tout entier car s'ils la définissent sur [0,2] par exemple, les minimums et maximums peuvent changer.
Edit: je vois que tu l'as fait au dessus, f(1)=-4 donc le minimum est -4. C'est-à-dire que c'est le point (1, -4) appartenant à la fonction f qui est situé le plus bas.
On cherchait pour quelle valeur de x, f'(x) = 0 on a trouvé 1 donc f'(1) = 0 c'est déjà fait.
Au fait vérifie dans l'énoncé que la fonction est définie sur IR tout entier car s'ils la définissent sur [0,2] par exemple, les minimums et maximums peuvent changer.
Edit: je vois que tu l'as fait au dessus, f(1)=-4 donc le minimum est -4. C'est-à-dire que c'est le point (1, -4) appartenant à la fonction f qui est situé le plus bas.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
