Arbre infini et espérance

[Mala]

EDITEDITEDIT

[L.A.]

Bonsoir.

Je suppose que ce n'est pas l'espérance de gain en euros que tu recherches, qui est 10 euros évidement parce que le jeu se termine toujours (avec probabilité 1) par un gain de 10 euros. Pour peu qu'on choisisse de rejouer indéfiniment, ce qui est ce qu'un joueur sensé fera puisqu'il n'a aucune raison de s'arrêter, c'est pourquoi je ne comprends pas pouquoi l'énoncé proposerait ce type de choix "crétin"...

Bref, si c'est le nombre de tirages moyen que tu cherches, tu peux commencer par calculer la probabilté que le joueur fasse plus de n tirages, qui correspond à la probabilité de tirer n-1 cartes noires successivement, et qui est en effet une suite géométrique.

[Mala]

Bonsoir.

Je suppose que ce n'est pas l'espérance de gain en euros que tu recherches, qui est 10 euros évidement parce que le jeu se termine toujours (avec probabilité 1) par un gain de 10 euros. Pour peu qu'on choisisse de rejouer indéfiniment, ce qui est ce qu'un joueur sensé fera puisqu'il n'a aucune raison de s'arrêter, c'est pourquoi je ne comprends pas pouquoi l'énoncé proposerait ce type de choix "crétin"...

Bref, si c'est le nombre de tirages moyen que tu cherches, tu peux commencer par calculer la probabilté que le joueur fasse plus de n tirages, qui correspond à la probabilité de tirer n-1 cartes noires successivement, et qui est en effet une suite géométrique.

Non non, c'est bien l'espérance de jeu que je cherche. Moi aussi je ne comprend pas trop la question. C'est ça qui me pose problème, évidement que l'esperance est de 10 c'est pour ça que je ne sais pas comment le démontrer

[L.A.]

Il faut passer par le lemme de Borel-Cantelli qui dit ici que le joueur qui choisit toujours de rejouer finira forcément (càd avec une probabilité 1) par tirer une carte rouge au bout d'un nombre fini de tirages. On en déduit que la variable aléatoire qui représente le gain du joueur est presque sûrement constante égale à 10 euros. L'espérance qui est son intégrale est donc celle d'une fonction constante égale à 10 sur un ensemble de mesure 1, soit 10 euros.

Mais je suis plutôt tiède sur le fait que ce soit bien ce qui est attendu ici, ça me semble un peu trop tortueux, et il reste ce "choix crétin" que je ne comprends pas bien... a priori le joueur peut aussi repartir avec 0 euros si il décide de s'arrêter avant de tirer une carte rouge. Pour en tenir compte dans le calcul de l'espérance, il faudrait donner une probabilité à ce choix : par exemple, il tire à pile ou face, il s'arrête s'il tombe sur pile et continue s'il tombe sur face.

A moins aussi que quelque chose ne m'échappe totalement, vu que je ne suis pas probabiliste... :triste:

[Mala]

Il faut passer par le lemme de Borel-Cantelli qui dit ici que le joueur qui choisit toujours de rejouer finira forcément (càd avec une probabilité 1) par tirer une carte rouge au bout d'un nombre fini de tirages. On en déduit que la variable aléatoire qui représente le gain du joueur est presque sûrement constante égale à 10 euros. L'espérance qui est son intégrale est donc celle d'une fonction constante égale à 10 sur un ensemble de mesure 1, soit 10 euros.

Mais je suis plutôt tiède sur le fait que ce soit bien ce qui est attendu ici, ça me semble un peu trop tortueux, et il reste ce "choix crétin" que je ne comprends pas bien... a priori le joueur peut aussi repartir avec 0 euros si il décide de s'arrêter avant de tirer une carte rouge. Pour en tenir compte dans le calcul de l'espérance, il faudrait donner une probabilité à ce choix : par exemple, il tire à pile ou face, il s'arrête s'il tombe sur pile et continue s'il tombe sur face.

A moins aussi que quelque chose ne m'échappe totalement, vu que je ne suis pas probabiliste... :triste:

Oui c'est clairement trop poussé pour mon niveau ^^

Je pensais plus par passé par une suite géométrique non?

[L.A.]

Oui, ce genre de suite pourrait tout naturellement intervenir quelque part dans ce genre de contexte, le "nombre de tirages" suit d'ailleurs une loi géométrique, mais l'espérance que tu cherches ici n'en utilise pas, elle contourne le problème justement...

Peut-être que tu pourrais préciser le contexte de l'exo s'il y en a, ou ce qu'est un cours "d'aide à la décision" en gros, c'est un peu mystérieux pour moi.

Ici on pourrait envisager que le joueur continue à chaque étape avec une même probabilité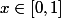 (par exemple x=1/2 si il tire ce choix à pile ou face), calculer l'esperance de gain
E(x) qui est une fonction de x (grâce à cette fameuse suite géométrique) et constater que cette espérance est maximale pour x = 1 (cas où le joueur continue à tous les coup).

Mais c'est une prise de liberté par rapport à l'énoncé de départ.

[L.A.]

J'ajoute une remarque : en fait, introduire un paramètre x comme je l'ai fait permettrait de démontrer que l'espérance est bien 10 euros sans passer par le lemme de Borel-Cantelli. Il faut juste prendre bien garde à la continuité de E(x) aux bornes de l'intervale 0 et 1.

[Mala]

J'ajoute une remarque : en fait, introduire un paramètre x comme je l'ai fait permettrait de démontrer que l'espérance est bien 10 euros sans passer par le lemme de Borel-Cantelli. Il faut juste prendre bien garde à la continuité de E(x) aux bornes de l'intervale 0 et 1.

Disons qu'il n'y à pas vraiment de contexte. Plein de notions interviennent dans ce cours. Ca va de la programmation linéaire à la théorie des graphes en passant justement par ce genre d'ovni probabiliste.

Les probas sont un lointain souvenir de mes cours de TS du coup je suis un peu paumé et le prof nous incite à nous débrouiller un peu par nous même... Sauf que pour le coup pour démontrer ça je n'y arrive pas du tout.

Je pense que ta prise de liberté est juste mais je n'arrive tout de même pas à comprendre ton raisonnement.

[Mala]

Mais c'est déjà très cool de m'aider et de prendre du temps pour moi !

[Mala]

Up

Je sent que j'approche du résultat ^^