Matrice
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Raphoul
- Membre Relatif
- Messages: 139
- Enregistré le: 30 Oct 2013, 11:14
-
 par Raphoul » 30 Mar 2014, 12:24
par Raphoul » 30 Mar 2014, 12:24
Bonjour
on considère la matrice

je devais calculer M^2 que j'ai fait et je trouve

et ensuite

et maintenant je dois factoriser

et en déduire que

est inversible ainsi que son inverse
ensuite je devais factoriser

, je trouve
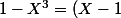(-X^2-X-1))
ou encore
(X^2+X+1))
donc je pose
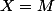
ca fait donc
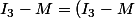(M^2+M+I_{3}))
comment en déduire que

est inversible et son inverse ?
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 30 Mar 2014, 12:29
par Robic » 30 Mar 2014, 12:29
Bonjour ! Tu as fait une erreur : ce n'est pas
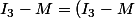(M^2+M+I_{3}))
mais
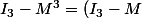(M^2+M+I_{3}))
. Du coup tu peux simplifier (vu que tu as calculé
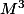
), et tu vas voir aussitôt l'inverse demandée.
Au cas où tu ne verrais toujours pas (mais à mon avis si), il suffit de recopier la définition du cours en l'adaptant à

: à quelle condition est-elle inversible ? S'il existe ta ta ta telle que

multipliée par ta ta ta est égale à ta ta ti, etc. etc.
-
Raphoul
- Membre Relatif
- Messages: 139
- Enregistré le: 30 Oct 2013, 11:14
-
 par Raphoul » 30 Mar 2014, 13:02
par Raphoul » 30 Mar 2014, 13:02
Robic a écrit:Bonjour ! Tu as fait une erreur : ce n'est pas
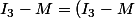(M^2+M+I_{3}))
mais
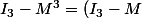(M^2+M+I_{3}))
. Du coup tu peux simplifier (vu que tu as calculé
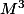
), et tu vas voir aussitôt l'inverse demandée.
Au cas où tu ne verrais toujours pas (mais à mon avis si), il suffit de recopier la définition du cours en l'adaptant à

: à quelle condition est-elle inversible ? S'il existe ta ta ta telle que

multipliée par ta ta ta est égale à ta ta ti, etc. etc.
oui c'est bon j'ai compris donc il reste
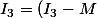(M^2+M+I_{3}))
une matrice A est inversible lorsque il existe une matrice B telle que AB=BA=In
mais quelle est la matrice A et B ici ?
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 30 Mar 2014, 15:32
par Robic » 30 Mar 2014, 15:32
Eh ben !
On te demande de démontrer que I-M est inversible. Donc A, c'est I-M, y'a pas le choix !
Donc il faut qu'il existe une matrice B telle que (I-M)B = B(I-M) = I. La question précédente fournit un candidat.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
mais
. Du coup tu peux simplifier (vu que tu as calculé
), et tu vas voir aussitôt l'inverse demandée.
: à quelle condition est-elle inversible ? S'il existe ta ta ta telle que
multipliée par ta ta ta est égale à ta ta ti, etc. etc.