Ex sur les suites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
arclite
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2006, 15:15
-
 par arclite » 10 Sep 2006, 15:25
par arclite » 10 Sep 2006, 15:25
Bonjour à tous, J'aurai vraiment besoin de votre aide pour un exercice sur les suites :
Soit Wn=n+5*(-1)^n
Etudier sa monotonie et ses limites en +00
Puis donner un contre exemple pour :
Une suite croissante majorée par 2 converge vers 2
Une suite Un convergente est à partir d'un rang, soit croissante majorée soit decroissante minorée.
Si Un est une suite divergente dont tous les termes sont non nul alors 1/Un converge.
Voilà pour la monotonie j'étudie Wn+1-Wn et je trouve
Wn+1-Wn=1>0 donc Wn est stric croissante. CE QUI ME SEMBLE FAUX, la suite me parait etre non monotone !!!
Help svp svp merci
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 10 Sep 2006, 15:32
par B_J » 10 Sep 2006, 15:32
Un n'est pas monotone mais admet une limite ( +infini ) en +infini ( mets n en facteur )
-
arclite
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2006, 15:15
-
 par arclite » 10 Sep 2006, 15:47
par arclite » 10 Sep 2006, 15:47
J'ai donc Wn= n[1+(5/n)*(-1^n)/n] mais (-1)^n/n tend vers 0 et 5/n vers +00
Il y a une forme indeterminée
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 10 Sep 2006, 15:57
par B_J » 10 Sep 2006, 15:57
c'est faux
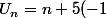^n=n[1+\frac{5(-1)^n}{n}])
-
arclite
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2006, 15:15
-
 par arclite » 10 Sep 2006, 16:04
par arclite » 10 Sep 2006, 16:04
oui c'est vrai, pardon.
Sinon pour prouver sa non monotonie il me suffit juste de dire que u(n)>u(n+1)>u(n+2) et inversement?
-
arclite
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2006, 15:15
-
 par arclite » 10 Sep 2006, 16:15
par arclite » 10 Sep 2006, 16:15
Enfin je veux dire que cette relation "u(n)>u(n+1)>u(n+2)"(ou le contraire) n'est pas valable ici, la suite n'est donc pas monotone non?
-
arclite
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2006, 15:15
-
 par arclite » 10 Sep 2006, 16:46
par arclite » 10 Sep 2006, 16:46
Pourriez-vous m'aidez pour cette afirmation:
Une suite Croissante majorée par 2 converge vers 2.
Je n'arrivepas a trouver un contre exemple. merci
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 10 Sep 2006, 16:51
par B_J » 10 Sep 2006, 16:51
la suite definie par
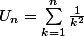
repond a ta question
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 152 invités
