Bonjour a tous,
j'ai du mal à répondre a cette question en la démontrant ,
Peut il exister sur un espace probabilisé, n événements P-indépedants de même probabilité p et dont la réunion est de probabilité 1 ?
Merci
Probabilité indépendance
12 messages
- Page 1 sur 1
hipstick a écrit:Bonjour a tous,
j'ai du mal à répondre a cette question en la démontrant ,
Peut il exister sur un espace probabilisé, n événements P-indépedants de même probabilité p et dont la réunion est de probabilité 1 ?
Merci
lancer un dé 6 faces numérotées 1 à 6 devrait le faire,
une loi de probabilité uniforme répond à cela ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Salut,
Je suis pas sûr de comprendre le sens du "P-indépendants"...
Dans le cas avec 2 évènements
avec 2 évènements  et
et  indépendants de même proba.
indépendants de même proba.  , tu veut que :
, tu veut que :
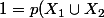=p(X_1)+p(X_2)-p(X_1\cap X_2)=p+p-p^2)
Ce qui signifie que , c'est à dire que
, c'est à dire que 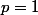
Sauf erreur, dans le cas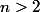 , tu aboutit au même résultat en utilisant le principe d'inclusion-exclusion si on suppose que les
, tu aboutit au même résultat en utilisant le principe d'inclusion-exclusion si on suppose que les  évènements sont globalement indépendants.
évènements sont globalement indépendants.
Je suis pas sûr de comprendre le sens du "P-indépendants"...
Dans le cas
Ce qui signifie que
Sauf erreur, dans le cas
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Salut,
Je suis pas sûr de comprendre le sens du "P-indépendants"...
Dans le casavec 2 évènements
et
indépendants de même proba.
, tu veut que :
Ce qui signifie que, c'est à dire que
Sauf erreur, dans le cas, tu aboutit au même résultat en utilisant le principe d'inclusion-exclusion si on suppose que les
évènements sont globalement indépendants.
Bonjour Ben314,
c'est le vocabulaire qui vous gène ou ce que cela veut dire ?
Ben, comme je fait pas trop la différence entre "c'est le vocabulaire qui me gène" et "c'est ce que ça veut dire que je comprend pas" :hein:hipstick a écrit:Bonjour Ben314,
c'est le vocabulaire qui vous gène ou ce que cela veut dire ?
on va dire... les deux...
Le seul truc qui me vient à l'esprit, c'est que "P-indépendantes", ça veuille dire indépendantes quand on les prend P par P... ç'est à dire que la proba de l'intersection de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Si c'est bien ça que ça veut dire, alors on peut par exemple trouver 3 évènements 2 à 2 indépendant, dont la proba de la réunion est 1 et qui soient tout les 3 de même proba  différente de 1 (c'est ça qui est pas évident dans ton énoncé : est-ce possible avec
différente de 1 (c'est ça qui est pas évident dans ton énoncé : est-ce possible avec  ?)
?)
Par contre, les 3 évènements seront forcément non globalement indépendants.
Exemple : tu jette deux fois une pièce (non truquée)
X1="la première pièce tombe sur pile"
X2="la deuxième pièce tombe sur pile"
X3="les deux pièces donnent le même résultat"
Par contre, les 3 évènements seront forcément non globalement indépendants.
Exemple : tu jette deux fois une pièce (non truquée)
X1="la première pièce tombe sur pile"
X2="la deuxième pièce tombe sur pile"
X3="les deux pièces donnent le même résultat"
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Ben, comme je fait pas trop la différence entre "c'est le vocabulaire qui me gène" et "c'est ce que ça veut dire que je comprend pas" :hein:
on va dire... les deux...
Le seul truc qui me vient à l'esprit, c'est que "P-indépendantes", ça veuille dire indépendantes quand on les prend P par P... ç'est à dire que la proba de l'intersection dedes événement est égal à
mais qu'au delà de P, çe ne soit pas forcément indépendant.
D'apres mon prof, en probabilité on dit plutot que deux événements sont p-independants et non pas indépendants d'apres lui. c'est pour ça que j'ai utiliser ce terme la. j'aurai pu dire indépendant aussi donc le probleme n'est pas la
Ben314 a écrit:Si c'est bien ça que ça veut dire, alors on peut par exemple trouver 3 évènements 2 à 2 indépendant, dont la proba de la réunion est 1 et qui soient tout les 3 de même probadifférente de 1 (c'est ça qui est pas évident dans ton énoncé : est-ce possible avec
?)
Par contre, les 3 évènements seront forcément non globalement indépendants.
Exemple : tu jette deux fois une pièce (non truquée)
X1="la première pièce tombe sur pile"
X2="la deuxième pièce tombe sur pile"
X3="les deux pièces donnent le même résultat"
Il faut que la réunion de ces événements soit de probabilité égale à 1
hipstick a écrit:Il faut que la réunion de ces événements soit de probabilité égale à 1
Ce qui... est le cas de mon exemple...
(si ni X1 ni X2 ne sont réalisé, c'est que le tirage est Face,Face et on est dans le cas X3)
D'ailleurs, plus généralement, si on fait n tirage et si, pour k entre 1 et n on note Xk="La k-ième pièce tirée a donnée Pile" ainsi que X(n+1)="Le nombre de Pile tiré est pair" alors :
1) Tout les Xk ont la même proba 1/2
2) Lorsque l'on ne prend que n des n+1 évènements, ils sont indépendants
3) La proba de la réunion de tout les Xk fait 1
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
hipstick a écrit:D'apres mon prof, en probabilité on dit plutot que deux événements sont p-independants et non pas indépendants d'apres lui. c'est pour ça que j'ai utiliser ce terme la. j'aurai pu dire indépendant aussi donc le probleme n'est pas la
Tu dira à ton prof. (de ma part) de regarder un peu les cours de proba (sur le net ou sur papier) pour voir combien il y en a qui utilisent le terme "p-indépendant"...
Je pense qu'il a voulu un peu trop abréger ce que l'on écrit en général "indépendants pour la probabilité p" et que l'on emploi lorsque l'on a plusieurs probabilités sur la même tribu
En résumé, si tu discute avec d'autres matheux que ton prof, emploie plutot le mot "indépendant" tout seul : ça permettra à celui qui te lit de comprendre :lol3:
Sinon, si tes évènement doivent être globalement indépendent, le principe d'inclusion-exclusion va impliquer que la proba. de chacun des évènement doit être égale à 1 (ce qui, réciproquement, implique qu'ils sont forcément indépendants et que la proba de la réunion fait 1)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
