Transformée de fourier
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
shami18
- Messages: 1
- Enregistré le: 16 Fév 2014, 06:01
-
 par shami18 » 16 Fév 2014, 06:28
par shami18 » 16 Fév 2014, 06:28
Bonsoir a tous,
J'ai besoin d'aide pour un probleme
Soit f une fonction lineaire sur R. tel que:
f(x)=0 si x >6 ou x<0
f(x) croit lineairement de 0 a y1 si 0f(x) croit lineairement de y1 a y2 si 1f(x) croit lineairement de y2 a y3 si 2f(x) decroit lineairement de y3 a y4 si 3f(x) decroit lineairement de y4 a y5 si 4f(x) decroit lineairement de y5 a 0 si 5Il ya une symmetrie selon la droite x=3
(Ps : j'ai essaye d'inclure une image mais j'ai pas compris comment faire)
je dois donc trouver la transformee de fourier de cette fonction.
La solution dit que f peut etre exprimer de la sorte :
f(x)= y1*;)(x-1)+y2*;)(x-2)+y3*;)(x-3)+y4*;)(x-4)+y5*;)(x-5) ou ;)(x) est la fonction triangle.
Je ne comprends pas cela.
Merci beaucoup a quiconque qui pourra m'expliquer pourquoi

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 17 Fév 2014, 10:50
par Ben314 » 17 Fév 2014, 10:50
Salut,
Si on pose (pour simplifier)
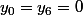
alors, sur l'intervalle
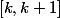
(où

) ta fonction varie de façon affine de
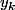
à
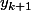
donc
=y_k+(x-k)(y_{k+1}-y_k))
Si

désigne l'indicatrice de la partie

de

, on a donc, pour tout réel x :
\ =\ \sum_{k=0}^{k=5}{\bb 1}_{[k,k+1[}(x)\Big((k+1-x)y_k+(x-k)y_{k+1}\Big))
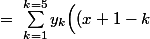{\bb 1}_{[k-1,k[(x)+(k+1-x){\bb 1}_{[k,k+1[}(x)}\Big)\)
Et, par linéarité de la transformée de fourrier, tu n'a plus qu'à calculer la transformée de fourier des "fonctions triangles"
{\bb 1}_{[k-1,k[(x)+(k+1-x){\bb 1}_{[k,k+1[}(x))
P.S. : Le fait qu'il y ait une symétrie par rapport à la droite
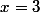
signifierais que
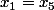
et
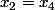
...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
