Traversée d'une rivière

[mydoudouitsk]

Bonjour, j'ai un gros souci de compréhension sur le passage d'une formule à une autre en cinétique.
Voici l'exercice et le passage que je ne comprends pas:

soit une rivière rectiligne suivant un vecteur ux(->), elle est de largeur L suivant un vecteur uy(->)
Un nageur part d'un point O (centre du repère (O,ux(->),uy(->)))§. Un point A est situé en face de O sur l'autre rive.

premièrement il nage perpendiculairement au courant tout en se laissant porter par l'eau, il arrive alors en un point B.

1.1- calculer le temps t1 de la traverser et le commenter.

j'ai réussi à écrire que ON(->)= (Vn.uy(->)+Ve.ux(->))t
J'ai donc dit que t= ON(->)/(Vn.uy(->)+Ve.ux(->)))

j'aperçois que uy devrait être égal à L pour t1

Mais la correction dit que t1=L/Vn
Où est passé Ve?
Comment peut-on établir cette relation? dans quelles circonstances?

Merci par avance pour votre aide!

[vingtdieux]

Déja mis sur un autre site. Enoncé mal écrit....

[mydoudouitsk]

Si je viens sur un forum ce n'est pas pour qu'on me donne une correction toute faite mais pour qu'on m'indique comment trouver la réponse grâce à de la logique, afin que je comprenne en écrivant et non en recopiant.
Mais merci quand même pour votre réponse.

[Mathusalem]

Tu peux tout bonnement te permettre de dire cela, parce que le nageur traverse la rivière avec une vitesse selon l'axe y qui est de Vn. Que la rivière le déporte ou pas, sa vitesse projetée sur y restera la même.. Il doit couvrir une distance L, il a une vitesse Vn. Pour arriver de l'autre côté de la rive, il a donc dû nager pendant t = L/Vn.

Tu as enfait écrit la même chose. Soit la déplacement le long de la rive la grandeur D.
On sait que D = Ve*t1 (la distance qu'il parcoure selon x a cause du fleuve jusqua ce qu'il arrive de l'autre côté

La longueur ON est de

De plus, la norme V de la vitesse est de
et 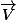sont colinéaires forcément,
Tu as t1 =



t1 =

Note : une division de vecteur n'a aucun sens. Le temps est une grandeur scalaire, ainsi, si tu veux trouver que le temps en fonction d'une distance et d'une vitesse, mais que ces dernières tu les as qu'en forme de vecteurs, tu vas devoir prendre leur normes afin d'avoir des scalaires. De plus, l'orientation relative de ceux-ci est également importante (c'est ce que tu prends en compte quand tu fais des projections). Donc quand je dis qu'ils sont colinéaires, je me permets de diviser la norme de l'un par l'autre, sans faire intervenir un quelconque cosinus dans le schmilblick.

[mydoudouitsk]

Magnifique!
effectivement la cinétique s'éclaire!
J'oublie malheureusement toujours de "re"composer les vecteur...
Bref merci beaucoup j'ai enfin compris la correction de cet exercice!
Très bonne continuation! Et merci de nous aider comme vous le faites!!! :we:

[mydoudouitsk]

De nouveau moi, j'espère que quelqu'un verra mon message.
J'ai poursuivi l'exercice et j'aimerai savoir si ce que j'ai écrit est juste...

suite de l'énoncé.

Dans un second temps le nageur développe sa nage de manière a avoir une trajectoire perpendiculaire aux berges, en arrivant ainsi au point A.

1. calculer le temps t2 de la traversée.

Voilà ce que j'ai écrit. les vecteurs sont en gras

Vn/T=Vn/e+Ve/T
V.uy=Vn.uy+Ve.ux
dOA=(Vn.uy+Ve.ux)dt

J'intègre de t=0 à t2

OA= Vn.uy.t2+Ve.ux.t2

or V²=Vn²+Ve²
donc





C'est ça ou je me suis plantée pour le choix de la vitesse dans la loi de composition des vitesses?

[Mathusalem]

Hmmm... Je ne sais pas, le nageur peut développer une vitesse maximale de nage de Vn non ?
Donc son vecteur vitesse est de taille Vn de toutes façons ?
Ce que tu cherches à savoir, c'est son orientation par rapport au courant de manière à ce que la contribution du fleuve soit nulle et qu'il nage perpendiculairement.

Entre autres, si tu poses pour l'angle entre et la vitesse, alors ta condition de nage perpendiculaire est
Vn*sin() = -Ve.
Ainsi, la vitesse normale Vnorm serait de Vn*cos dans la direction normale ()

Tu peux trouver theta en fonction de Vn et Ve, tu substitues dans la deuxième équation, car celle là te donne t2 = L/Vnorm