Bonjour, je suis en train de faire un exercice de cinématique et un correction me pose problème pourriez vous me l'expliquer?
Les vecteur sont en gras
on pose un point M repéré par ses coordonnées polaires r et O(thêta) tel que OM=r.ur et (ux ,ur)=O(thêta) (axe polaire Ox) parcourt une spirale logarithmique d'équation polaire r=r0.exp(O)
La vitesse angulaire est constante.
on me demande d'exprimer la vitesse du point M, ce qui me semblait plutôt simple.
Or le rayon n'est pas constant.
et il dise que dr/dt=(dr/dO).(dO/dt) O(thêta)
pour ensuite dire que dr/dO=r0.exp(O) et c'est la que je ne comprends pas. Pourriez vous m'expliquer?
Point mobile sur une spirale logarithmique
3 messages
- Page 1 sur 1
Si je te dis qu'en coordonnées polaires, les expressions générales de la position et de la vitesse sont :


Tu ne devrais pas être choqué.
La contrainte est que
Ainsi,
Donc ton problème est entièrement déterminé par la fonction) . En effet, vu la contrainte sur r, si tu connais
. En effet, vu la contrainte sur r, si tu connais ) , tu connais aussi r(t). Et donc tu pourras dériver par rapport au temps pour trouver
, tu connais aussi r(t). Et donc tu pourras dériver par rapport au temps pour trouver  et
et 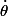 qui sont les dérivées temporelles de r et
qui sont les dérivées temporelles de r et  respectivement. Or tu ne connais pas explicitement la dépendence au temps de r(t) , donc
respectivement. Or tu ne connais pas explicitement la dépendence au temps de r(t) , donc  se récrit
se récrit  . Ici tu vois denouveau qu'il te suffit de connaitre
. Ici tu vois denouveau qu'il te suffit de connaitre ) est t'as tout résolu.
est t'as tout résolu.

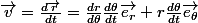
Tu connais la dépendence de r en de la contrainte qu'on te donne. Et comme Olympus de l'a expliqué,
de la contrainte qu'on te donne. Et comme Olympus de l'a expliqué, 

Maintenant, tu peux comprendre les choses : est une fonction du temps à priori, et r est une fonction de
est une fonction du temps à priori, et r est une fonction de  . C'est comme la composition de fonctions. Quand tu d\'erives
. C'est comme la composition de fonctions. Quand tu d\'erives
^3) par rapport à x,
par rapport à x,
tu dérives d'abord
 = t^3) par rapport à t (où
par rapport à t (où  )
)
Ensuite = x^2 + 3) par rapport à x.
par rapport à x.
Donc,^3' = 3(x^2 +3)^2*[2x])
Le [2x] correspond à la dérivée interne, et dans ton problème initial, correspond à . [t^3] correspond à r(
. [t^3] correspond à r( ) =
) =
Ensuite, en ce qui concerne la physique, il est clair que tu ne peux pas dans ce problème avoir une expression explicite de la vitesse en fonction du temps. C'est impossible. Tu connais uniquement le chemin emprunté par la particule (i.e la contrainte). Aucune information n'est donnée sur les forces qui agissent sur lui, donc rien ne te permet de déterminer) , et donc ta vitesse explicite.
, et donc ta vitesse explicite.
J'espère avoir été clair
EDIT: Remarque que la vitesse, en remplaçant r par son expression, s'écrit :
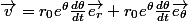
Tu ne devrais pas être choqué.
La contrainte est que
Ainsi,
Donc ton problème est entièrement déterminé par la fonction
Tu connais la dépendence de r en
Maintenant, tu peux comprendre les choses :
tu dérives d'abord
Ensuite
Donc,
Le [2x] correspond à la dérivée interne, et dans ton problème initial, correspond à
Ensuite, en ce qui concerne la physique, il est clair que tu ne peux pas dans ce problème avoir une expression explicite de la vitesse en fonction du temps. C'est impossible. Tu connais uniquement le chemin emprunté par la particule (i.e la contrainte). Aucune information n'est donnée sur les forces qui agissent sur lui, donc rien ne te permet de déterminer
J'espère avoir été clair
EDIT: Remarque que la vitesse, en remplaçant r par son expression, s'écrit :
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
