Bonjour
J'ai du mal à appliquer les notions d'équations différentielle vue en mathématiques en physique.
Que ce soit en mécanique ou en électrocinétique.
Je pense que ce qui me bloc c'est la différence de variable.
Pourriez-vous m'aider ?
Cordialement
Physique et equaton différentielle
5 messages
- Page 1 sur 1
Salut !
Dans ton équation :
[CENTER]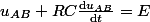 ,[/CENTER]
,[/CENTER]
tu as :
- une fonction : la tension dépendant du temps
dépendant du temps  ;
;
- trois constantes ,
,  et
et  .
.
De plus, en physique désigne ni plus ni moins que
désigne ni plus ni moins que ) , la dérivée de la fonction
, la dérivée de la fonction  .
.
Donc si l'on était en mathématiques, on poserait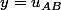 et
et 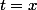 (
( serait alors une fonction de
serait alors une fonction de  ), et on aurait à résoudre l'équation différentielle :
), et on aurait à résoudre l'équation différentielle :
[CENTER]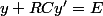 ,[/CENTER]
,[/CENTER]
que l'on préfèrera noter :
[CENTER]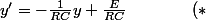) .[/CENTER]
.[/CENTER]
Des théorèmes que tu as vu (ou verras) te diront que cette équation différentielle admet comme solution l'ensemble des fonctions de la forme :
[CENTER]= ke^{ - \frac{1}{RC}x} + E) ,[/CENTER]
,[/CENTER]
où est une constante réelle à déterminer suivant la donnée d'un condition initiale.
est une constante réelle à déterminer suivant la donnée d'un condition initiale.
Considérons à présent l'équation :
[CENTER]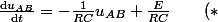) .[/CENTER]
.[/CENTER]
Bon, en physique, j'avais vu qu'on pouvait résoudre l'équation différentielle) de la manière suivante : on considère l'équation dite homogène (**) de (*) (elle ne contient plus le terme constant
de la manière suivante : on considère l'équation dite homogène (**) de (*) (elle ne contient plus le terme constant  ) :
) :
[CENTER]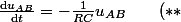) .[/CENTER]
.[/CENTER]
On a alors :
[CENTER]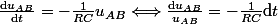 .[/CENTER]
.[/CENTER]
Ensuite, par passage à l'intégrale :
[CENTER]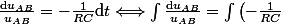 {\rm d}t \Longleftrightarrow \ln(|u_{AB}|) = - \frac{1}{RC} \int {\rm d}t = - \frac{1}{RC} t + k') ,[/CENTER]
,[/CENTER]
avec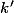 une constante réelle.
une constante réelle.
Ensuite, par passage à l'exponentielle, on en déduit que :
[CENTER]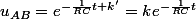 [/CENTER]
[/CENTER]
où est la constante réelle obtenue en posant
est la constante réelle obtenue en posant 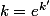 .
.
On a donc toutes les fonctions solution de) .
.
Ensuite, il suffit de remarque que si l'on considère la fonction comme constante alors d'après
comme constante alors d'après ) ,
, 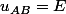 . Donc finalement, l'ensemble des solutions de l'équation (*) sont de la forme
. Donc finalement, l'ensemble des solutions de l'équation (*) sont de la forme =ke^{ - \frac{1}{RC} } + E) , où
, où  est une constante à déterminer si on connait une condition initiale (
est une constante à déterminer si on connait une condition initiale (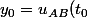) ).
).
En résumé, si on note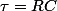 (constante de temps d'un dipôle RC), on a
(constante de temps d'un dipôle RC), on a  est solution de l'équation
est solution de l'équation 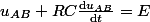 si et seulement si
si et seulement si  est de la forme
est de la forme =ke^{- \frac t {\tau}} +E,k) constante.
constante.
En espérant t'avoir aidé :+++: (ça remonte pour moi la physique).
Dans ton équation :
[CENTER]
tu as :
- une fonction : la tension
- trois constantes
De plus, en physique
Donc si l'on était en mathématiques, on poserait
[CENTER]
que l'on préfèrera noter :
[CENTER]
Des théorèmes que tu as vu (ou verras) te diront que cette équation différentielle admet comme solution l'ensemble des fonctions de la forme :
[CENTER]
où
Considérons à présent l'équation :
[CENTER]
Bon, en physique, j'avais vu qu'on pouvait résoudre l'équation différentielle
[CENTER]
On a alors :
[CENTER]
Ensuite, par passage à l'intégrale :
[CENTER]
avec
Ensuite, par passage à l'exponentielle, on en déduit que :
[CENTER]
où
On a donc toutes les fonctions solution de
Ensuite, il suffit de remarque que si l'on considère la fonction
En résumé, si on note
En espérant t'avoir aidé :+++: (ça remonte pour moi la physique).
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
