Pas de soucis.
J'omets la puissance 6 dans ce qui suit.
Tu as au temps t = 0 N(0) = 10.
Comment évolue ce nombre au cours du temps ? On te donne un modèle :
Si je te donne le nombre de particules à un temps T, alors je peux te dire combien y en aura (environ)

T plus tard, c'est à dire que je connais une relation entre N(T+

T) et N(T)
Cette relation, c'est N(T +

T) = N(T) +

N =
}_{\text{quantit\'e de base}} - \underbrace{\lambda*N(T)*\Delta T}_{\text{quantit\'e qui est morte entre T et T + \Delta T}})
Donc, on commence en T = 0
N(0) = 10
N(2) = N(0) - 0.18*N(0)*2 = 6.4
N(4) = N(2) - 0.18*N(2)*2 = 4.096
etc...
Quand on dit qu'on prend un pas de temps de 2, ça veut dire qu'on avance vers la solution distante de 2, par rapport à où l'on se trouve. On ne va pas calculer
N(4) = N(0) - 0.18*N(0)*4 = 2.8
Parce que ca voudrait dire que le pas de temps est de 4. Et tu peux te rendre compte que 4.096 n'est pas égal a 2.8.
Il s'avère que plus le pas de temps que tu choisis pour trouver tes valeurs est petit, plus tu seras précis.
Imagine que tu veuilles approcher la valeur de f(20) en partant de f(1), sachant que f(x) = x^2
(Dans ton exemple, on connaît pas N(t), juste son équa diff qu'on n'a pas résolu, donc imagine toi que là on connaît pas f(x))
Tu pourrais dire bon f(1) = 1
Je prends un pas de 'distance'

X = 1 et je dis que l'augmentation de ma fonction

F = f(x)';)X (graphiquement ça te fait le côte vertical du triangle généré par

X et la tangente à la courbe en x)
Donc je dis f(x +

x) = f(x) + f'(x);)X (tu remarqueras quelque chose pour la limite quand

X tend vers 0, et pourquoi le signe = devrait enfait être
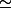
)
Et je calcule :
f(1) = 1
f(2) = 1 + 2*1 = 3
f(3) = 3 + 4*1 = 7
f(4) = 7 + 6*1 = 13
f(5) = 13 + 8*1 = 22
Mais bon, tu vois que 22 n'est pas égal 5^2
Tu peux refaire cet exemple pour toi avec

X = 0.5, et tu verras ce que tu obtiens pour f(5) en partant de f(1). Ca sera mieux.

