
Surtout pour les question 1,2,4,j'ai rien compris.

Sake a écrit:C'est plutôt intuitif, tu ne penses pas ?
1) Les plans passant par l'axe et tout plan orthogonal à l'axe (la longueur de la gaine est infinie donc il n'y a pas d'effets de bord) sont des plans de symétrie de la distribution, donc le champ est formé de vecteurs appartenant aux intersections de ces plans : Le champ électrostatique est radial.
En raison du caractère invariant par translation selon e_z, le champ ne dépend pas de z, et puisque le problème est le même par rotation d'un angle quelconque autour de l'axe, il ne dépend pas de theta non plus : E = E(r) e_r.
2) Utilise tout simplement le théorème de Gauss sur un volume bien défini.
4) Intègre la densité d'énergie électrostatique sur un volume de vide de hauteur L compris entre le cylindre et la gaine.
Sake a écrit:Merci, c'est gentilPasse un joyeux Noël toi aussi



 .
.Sake a écrit:Salut,
*Cachez-moi ces ongles que je ne saurais voir !*
Dans la question 1, ton/ta camarade a omis de préciser ce qui fait que le champ ne dépend que de r, mais de toute façon tu retrouveras l'explication dans mon premier message.
La question 2 est plutôt bien menée, même si la rédaction aurait pu être plus concise. J'ai été un peu vite sur les calculs, mais ils devraient être bons car le principe de superposition est respecté et la continuité du champ a été vérifiée.
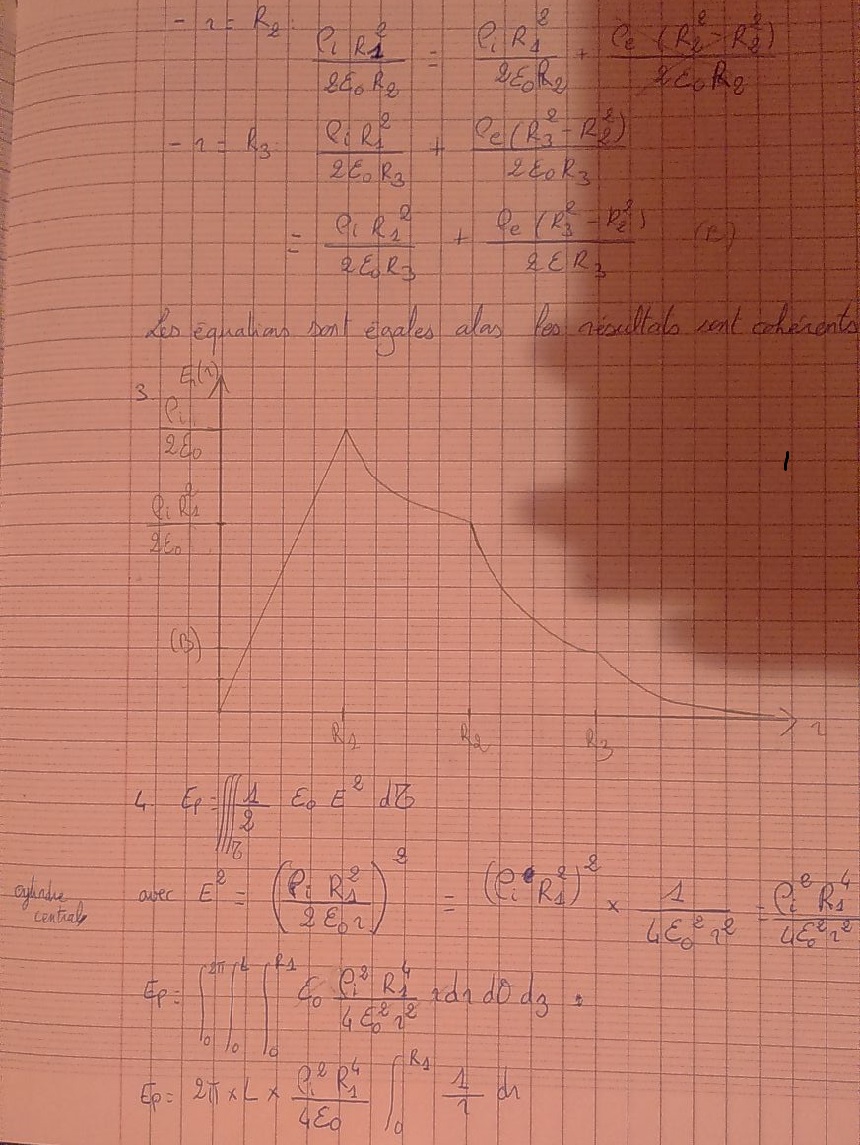
La question 3 est en fait la plus facile. A la lumière de ce qui a été fait dans la qu.2, ce devrait être une formalité : Pour r < R1, on sait que le champ varie linéairement, et qu'il atteint son max en R1 de telle manière que(il y a d'ailleurs une petite coquille dans ton "corrigé" à cet égard).
Le champ varie ensuite en 1/r, ce qui est le cas dans chacune des autres situations, d'où le graphe qui est ici dessiné !
D'ailleurs, on te demande une allure, il ne faut pas que ton dessin renseigne l'ensemble des comportements analytiques de la courbe. De fait, on s'attend à ce que le tracé présente un comportement en r, puis en 1/r dans chaque portion du domaine correspondant. Point.
En ce qui concerne la dernière question, ton ami(e) a oublié de rajouter un facteur 1/2. De même, son choix pour E n'est pas cohérent avec les bornes d'intégration choisies : On cherche à déterminer l'énergie portée par le cylindre central, donc il est pertinent d'intégrer entre 0 et R1. Ce qui est déconcertant, c'est de prendre pour autant l'expression de E pour R1r
R2...
Jjl a écrit:Oui les ongles j'ai oublié de les retiré,mais c'est pas les miens tkt,je ne suis pas assez efféminé pour avoir des ongles comme ça ^^,c'est bien ceux d'une amie pas un ami Dieu merci!
Ensuite les premières questions t'as bien expliqué donc ça ira,c'est le corrigé du prof,mais il n'a pas fais la question 4,comme tu dis,elle aurait du prendre l'expression pour r<R1 je lui ferai la remarque.
Je posterai un autre exo du même type mais plus simple plus tard pour être sûr d'avoir compris,en tout cas merci pour ton aide Sake.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Identification
Pas encore inscrit ?
Ou identifiez-vous :