Bonjour !
Voila j'ai lu quelques articles sur ce condensat mais je n'ai pas tout compris : j'ai compris que tout les bosons était dans le même état quantique( d'ailleurs je voudrais bien connaitre tous les paramètres d'un état quantique si quelqu'un les connait tous :) ) mais ce que je ne comprend pas, c'est que tout ces bosons se réunissent-ils ? Se rapprochent-ils ? Se superposent-ils ?
Merci de répondre à ma question :)
PS : il est possible que je ne puisse me connecter avant début Aout, je vous prie de m'en excuser mais je reviendrai sans fautes pour voir la réponse et surement participer au forum :)
Condensat de Bose-Einstein
3 messages
- Page 1 sur 1
D'abord,
Etat classique : paramètres définissant la particule.
L'état dépend de la particule étudiée et du potentiel dans lequel elle est plongée
ainsi que de son état initial.
(t,x,E,p) définit une particule
(t1,t2,x1,x2,E1,E2,p1,p2) définit un système à 2 particules
...
Etat quantique : paramètres définissant la fonction d'onde.
L'état dépend de la particule étudiée et du potentiel dans lequel elle est plongée
ainsi que de son état initial.
exemple : une particule sans spin dans une boîte 1d de longueur L
les états (stationnaires) sont :
 = \sum_n a_n exp(-i n \pi x/L))
l'état (stationnaire) est défini par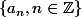
avec (une seule particule)
(une seule particule)
si l'on mesure la quantité de mouvement p de la particule,
nous allons trouver une valeur propre de l'opérateur
 \frac{\part \phi}{\part x} = p \phi)
soit par exemple : (-i n \pi/L) = p_n)
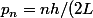)
avec une probabilité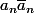 d'obtenir ce résultat.
d'obtenir ce résultat.
avec plusieurs particules, il n'y a qu'une seule fonction d'onde)
et donc des états quantiques dans lesquels il est impossible de séparer les particules.
sauf cas particulier où les particules sont indépendantes (séparables) :
 = \phi_1(x_1) . \phi_2(x_2))
Quand plusieurs particules sont dans le même état quantique,
tout ce que l'on peut dire est que le nombre d'occupation de cet état est n
(où n est le nombre de particules)
comme les particules sont identiques on ne peut pas dire où est l'une et où est l'autre :
la question n'a pas de sens.
Par ailleurs la probabilité pour un boson de se retrouver
dans un état déjà occupé par n autres bosons identiques
est (n+1) fois plus importante que celle de se retrouver
dans un état vide (sans aucun boson).
Etat classique : paramètres définissant la particule.
L'état dépend de la particule étudiée et du potentiel dans lequel elle est plongée
ainsi que de son état initial.
(t,x,E,p) définit une particule
(t1,t2,x1,x2,E1,E2,p1,p2) définit un système à 2 particules
...
Etat quantique : paramètres définissant la fonction d'onde.
L'état dépend de la particule étudiée et du potentiel dans lequel elle est plongée
ainsi que de son état initial.
exemple : une particule sans spin dans une boîte 1d de longueur L
les états (stationnaires) sont :
l'état (stationnaire) est défini par
avec
si l'on mesure la quantité de mouvement p de la particule,
nous allons trouver une valeur propre de l'opérateur
soit par exemple :
avec une probabilité
avec plusieurs particules, il n'y a qu'une seule fonction d'onde
et donc des états quantiques dans lesquels il est impossible de séparer les particules.
sauf cas particulier où les particules sont indépendantes (séparables) :
Quand plusieurs particules sont dans le même état quantique,
tout ce que l'on peut dire est que le nombre d'occupation de cet état est n
(où n est le nombre de particules)
comme les particules sont identiques on ne peut pas dire où est l'une et où est l'autre :
la question n'a pas de sens.
Par ailleurs la probabilité pour un boson de se retrouver
dans un état déjà occupé par n autres bosons identiques
est (n+1) fois plus importante que celle de se retrouver
dans un état vide (sans aucun boson).
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
