Célérité onde US dans de la mousse

[Zweig]

Salut,

Je me remets un peu aux ondes et comme je n'arrive pas à retrouver mes cours, j'ai quelques trous au niveau des formules ...

On dispose d'un montage émetteur-récepteur qui envoit des ondes ultra-sonores, le tout relié à un oscillo. Ils sont distant de r tels que les signaux soient en phase. Entre les deux, on place de la mousse d'épaisseur e et on me demande de déterminer la célérité de l'onde dans la mousse.

Une piste ?

(Bon avant on me demande de prédire ce qu'on verra sur l'oscillo lorsque que l'on va placer la mousse ... Je suppose que les signaux ne vont plus être en phase à cause de la mousse (la célérité dépend du milieu traversé))

[Zweig]

Je pense avoir trouvé. Déjà, où en fait on doit exprimer t avec des choses connues. Sachant la célérité (qu'on a déjà mesuré précédemment) de l'onde dans l'air, on sait à quel temps 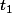elle arrive au récepteur. Du coup, si on sait à quel temps 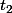l'onde arrive au récepteur en présence dans la mousse, on a le temps passé dans la mousse. En gros, suffit de déterminer via l'oscillo le déphasage, soit ?

[Mathusalem]

Salut, je comprends pas le montage. Y a-t-il deux émetteurs ? Je comprends pas ce qui vient en phase avec quoi.

Autrement, effectivement la vitesse est constante à travers le milieu.

Ainsi, entre un signal qui ne traverse pas la mousse et un signal qui traverse la mousse, il y aura au recepteur une différence de 'pas d'onde'.
Si on appelle v la vitesse du son dans l'air, c la vitesse du son dans la mousse, e l'epaisseur de la mousse, alors l'onde qui traverse la mousse aura passé au total un temps t = e/c dans la mousse.
Si on imagine deux ondes en phase, l'une entrant dans la mousse mais l'autre pas, celle dans la mousse 'recule' par rapport à l'autre d'une distance d = (v-c)*e/c

Si t'appelles x la direction de propagation de l'onde, tu as après la mousse l'onde qui n'a pas traversé la mousse

Celle qui a traversé

Ainsi tu vois que le déphasage entre les deux ondes vaut et tu connais k grâce à la relation de dispersion du son dans l'air w(k) (je suppose que tu connais la fréquence donc la pulsation).
Donc si t'as un moyen de mesurer c'est gagné.

Il est tard, donc sous réserve de fautes. Et je sais pas si j'ai compris ce que tu voulais. En espérant que ça aide

PS: Ta formule colle pas dimensionnellement, t'as du temps avec l'inverse d'une vitesse.

[Zweig]

Salut,

Voici l'énoncé complet (je vérifierai tes calculs demain) :

Emetteur à ultra-son séparé d'une distance r d'un récepteur, chacun relié à un oscilloscope.
L'émetteur émet un son sinusoïdal. r est tel que le son émis et le son réçu soient en phase.

On place une couche de mousse d'épaisseur e entre l'émetteur et le récepteur.

Calculer la célérité Cm de l'onde sonore dans la mousse (cela doit être déduit du déphasage des deux courbes mesuré via l'oscillo)

[Benjamin]

Salut,

Mathusalem a déjà dit beaucoup de choses. La grandeur vibratoire de ton onde peut s'exprimer s= A*cos(wt-kx+phi). Le mieux, c'est de passer dans le domaine complexe.
s devient S_ et s = Re(S_). Tu as alors S_ = A*exp(j*(wt-kx+phi)). Comme la fréquence est constante pendant tout le problème, on vire le exp(jwt) pour ne travailler que sur l'amplitude complexe du signal.
De plus, quitte à choisir une bonne origine, on peut supposer que phi = 0 au niveau de l'émetteur.

Tu as donc Se_0 = A, Se_(x) = A*exp(-jkx) et Se_r = Se_(r) = A*exp(-jkr) = A d'après l'énoncé car E et R sont placés tels que les signaux soit en phase.

Tu as donc kr = 0 [2 PI].

k est le nombre d'onde est vaut k = 2PI / lambda = w / v avec w la pulsation et v la vitesse de l'onde dans le milieu de propagation.

Quand tu mets une mousse sur le trajet, tu as :
Un trajet sans mousse qui vaut r-e, et un trajet avec mousse qui vaut e. Au niveau de R, tu as donc Se_r(mousse) = A * exp(-j[k(r-e)+kmousse*e]).

Tu as k(r-e)+kmousse*e = dephasage_mesure_a_l'oscillo [2 PI].
On a vu que kr = 0 [2 PI] et donc e * (kmousse - k) = dephasage_mesure_a_l'oscillo [2 PI].

Tu vois que kmousse est connu à modulo qqch. Cela te donne une condition sur l'épaisseur e pour effectivement mesuré la vitesse dans la mousse et ne pas te faire avoir. Si ta mousse est trop grande, tu mesures un déphasage de par exemple 45° alors qu'en réalité, il est de 45+360°.

A+

[Black Jack]

vitesse de l'onde dans l'air : 340 m/s (environ)

vitesse de l'onde dans la mousse : v1
*****

r (en m) = multiple de longueur d'onde.

Sans mousse : durée du trajet de l'onde entre émetteur et récepteur : t1 = r/340

Avec mousse: durée du trajet de l'onde entre émetteur et récepteur : t2 = (r-e)/340 + e/v1

t2 - t1 = -e/340 + e/v1 = e.(1/v1 - 1/340)

C'est le déphasage en temps du à la mousse entre les signaux émetteur et récepteur.

En degrés entre les sinusoïdes, on a donc Phi = 360/T * e.(1/v1 - 1/340)

Phi = 360.f.e.(1/v1 - 1/340)

En connaissant f (en Hz) et e (en m) et en mesurant Phi (en °), on peut donc calculer v1 (en m/s)

Il faut quand même prendre garde que Phi est mesuré à 2Pi près et donc il est souhaitable de faire des mesures avec plusieurs e et réfléchir un peu pour ne pas se planter.

Réfléchir aussi au "sens" du déphasage (avance ou retard du récepteur par rapport à l'émetteur) pour mettre le signe adéquat à Phi.

:zen:

[Zweig]

Merci pour vos explications ;-) !