Bonjour,
J'ai un soucis ac la correction du prof ...
J'ai dw = dS*cos ;) / r2
On a S1 = 10^-3 m² surface émetteur et on doit calculer les Angles solides vu par lemetteur sachant que
S2 est placé a 150 dans le sens trigo
S3 a 90
S4 a 45
Et les 3 surfaces sont égales a S1
Et il dis que w2-1 = w3-1 .. Je comprend pas surtout qu'après il s'en est resservi pr calculer le flux intercepte par les surfaces..
Merci
Angle solide
12 messages
- Page 1 sur 1
Mathusalem a écrit:Je suppose aussi que ces surfaces sont equidistantes au sens de la normale à leur surface non ? C'est à dire à partir du point sur S1 (dont l'aire t'es inutile de ce que je comprends), le rayon qui coupe à angle droit les surfaces S2 S3 et S4 est de longueur égale pour chaque surface, non ?
je comprend pas... tanpis j'improviserais lol...
As-tu bien conscience de ce qu'est un angle solide ?
Un angle dans un plan, c'est le rapport L/r, où L est la longueur de l'arc de cercle (cercle de centre le point d'observation et de rayon r) intercepté par le demi-droite formant l'angle. On montre que cet angle est indépendant du rayon r, puisque L augmente en même temps que r de manière proportionnel à l'angle justement.
L'angle solide, c'est la même chose dans l'espace. C'est le rapport S/r² où S est la superficie de la surface de la calotte sphérique (sphère de centre le point d'observation et de rayon r) interceptée par le solide (une sorte de cone) qui part du point d'observation et qui est formé de ces génératrices (désolé, c'est peut-être pas très clair :s). Et là, aussi, c'est indépendant de r.
Bref, pour prendre un exemple, si on se place en coordonnées sphériques, tu prends l'élément de surface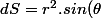.d\theta d\phi) et donc
et donc 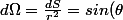.d\theta d\phi) . En découpant judicieusement et en prenant les bonnes bornes d'intégration, tu peux déterminer tes angles solides. L'angle solide sous lequel est vu un objet depuis un point d'observation (il s'agit bien d'un point, c'est pour ça que Math disait que la surface S1 ne servait à rien) dépend donc de la forme, de la taille, de l'orientation, et de l'éloignement de l'objet.
. En découpant judicieusement et en prenant les bonnes bornes d'intégration, tu peux déterminer tes angles solides. L'angle solide sous lequel est vu un objet depuis un point d'observation (il s'agit bien d'un point, c'est pour ça que Math disait que la surface S1 ne servait à rien) dépend donc de la forme, de la taille, de l'orientation, et de l'éloignement de l'objet.
D'ailleurs, en intégrant sur tout l'espace l'équation précédente, on voit que l'angle solide de l'espace entier et 4PI stéradian. Si on se replace en 2D, on trouvera que l'angle plat fait 2PI radians, chose rassurante !
Un angle dans un plan, c'est le rapport L/r, où L est la longueur de l'arc de cercle (cercle de centre le point d'observation et de rayon r) intercepté par le demi-droite formant l'angle. On montre que cet angle est indépendant du rayon r, puisque L augmente en même temps que r de manière proportionnel à l'angle justement.
L'angle solide, c'est la même chose dans l'espace. C'est le rapport S/r² où S est la superficie de la surface de la calotte sphérique (sphère de centre le point d'observation et de rayon r) interceptée par le solide (une sorte de cone) qui part du point d'observation et qui est formé de ces génératrices (désolé, c'est peut-être pas très clair :s). Et là, aussi, c'est indépendant de r.
Bref, pour prendre un exemple, si on se place en coordonnées sphériques, tu prends l'élément de surface
D'ailleurs, en intégrant sur tout l'espace l'équation précédente, on voit que l'angle solide de l'espace entier et 4PI stéradian. Si on se replace en 2D, on trouvera que l'angle plat fait 2PI radians, chose rassurante !
Benjamin a écrit:As-tu bien conscience de ce qu'est un angle solide ?
Un angle dans un plan, c'est le rapport L/r, où L est la longueur de l'arc de cercle (cercle de centre le point d'observation et de rayon r) intercepté par le demi-droite formant l'angle. On montre que cet angle est indépendant du rayon r, puisque L augmente en même temps que r de manière proportionnel à l'angle justement.
L'angle solide, c'est la même chose dans l'espace. C'est le rapport S/r² où S est la superficie de la surface de la calotte sphérique (sphère de centre le point d'observation et de rayon r) interceptée par le solide (une sorte de cone) qui part du point d'observation et qui est formé de ces génératrices (désolé, c'est peut-être pas très clair :s). Et là, aussi, c'est indépendant de r.
Bref, pour prendre un exemple, si on se place en coordonnées sphériques, tu prends l'élément de surfaceet donc
. En découpant judicieusement et en prenant les bonnes bornes d'intégration, tu peux déterminer tes angles solides. L'angle solide sous lequel est vu un objet depuis un point d'observation (il s'agit bien d'un point, c'est pour ça que Math disait que la surface S1 ne servait à rien) dépend donc de la forme, de la taille, de l'orientation, et de l'éloignement de l'objet.
D'ailleurs, en intégrant sur tout l'espace l'équation précédente, on voit que l'angle solide de l'espace entier et 4PI stéradian. Si on se replace en 2D, on trouvera que l'angle plat fait 2PI radians, chose rassurante !
moué mais dans mon cours j'ai juste dw = ds cos a / r², oki je vois à peu prés!
D'ailleurs, c'est comme ça tu prouves que le flux electrique d'une charge ponctuelle hors d'un volume à travers une surface fermée de ce volume est nul.
Prends la définition du flux
1.
où est l'élément de surface orienté. Par définition de E, ceci se récrit
est l'élément de surface orienté. Par définition de E, ceci se récrit
2.
Or, le produit scalaire entre et
et 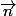 où n est l'orientation exterieure de la surface, c'est
où n est l'orientation exterieure de la surface, c'est ) où
où  est l'angle entre
est l'angle entre  et
et 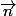
On voit bien que) est l'élément de surface projeté sur le plan orthogonal au rayon.
est l'élément de surface projeté sur le plan orthogonal au rayon.
On a bien une définition d'angle solide
3.}{r^2})
4.
C'est l'intégrale sur la surface fermée. Le champ pénètre un bout de surface, et son intégrale vaut (4.). Le champ continue et pénètre le bout de surface suivant. Là, le produit scalaire entre et
et 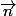 change de signe, et donc le flux à travers cette surface vaut -(4.). Toutes les composantes rentrantes s'annulent avec les composantes sortantes.
change de signe, et donc le flux à travers cette surface vaut -(4.). Toutes les composantes rentrantes s'annulent avec les composantes sortantes.
Donc le flux electrique a travers une surface fermée est nul, pour autant que l'origine de ce flux soit externe a la surface.
EDIT : Remarque, (3.) correspond à ta définition.
Prends la définition du flux
1.
où
2.
Or, le produit scalaire entre
On voit bien que
On a bien une définition d'angle solide
3.
4.
C'est l'intégrale sur la surface fermée. Le champ pénètre un bout de surface, et son intégrale vaut (4.). Le champ continue et pénètre le bout de surface suivant. Là, le produit scalaire entre
Donc le flux electrique a travers une surface fermée est nul, pour autant que l'origine de ce flux soit externe a la surface.
EDIT : Remarque, (3.) correspond à ta définition.
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

