Conditions d'equilibre d'un solide

[Anonyme]

Bonsoir,

Est ce quelqu'un peut m'expliquer pourquoi pour qu'un solide soit en équilibre sous l'action de trois forces F1, F2 et F3 il faut que celle ci soient concourantes, coplanaires.

Merci

[Sa Majesté]

Salut

Tu as

donc

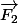Le vecteur est dans le plan formé par et donc 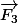l'est aussi

Quant à concourantes, c'est une histoire de moment. Imagine seulement 2 forces qui agissent sur un solide et dont la somme est nulle. Si elles ne sont pas concourantes alors le solide va tourner donc il ne sera pas en équilibre.

[Anonyme]

Merci en fait c'est juste le fait qu'elles doivent être concourante qui me pose problème. Pour la situation avec deux force ça va j'arrive bien a comprendre pourquoi mais pour 3 forces j'arrive pas pourrais tu un peu plus m'expliquer ou me démontrer cela logiquement ou par calcul ?

[Anonyme]

up personne ?

[fal]

en pratique; il suffit de suspendre à un support une plaque plane sous l'effet de trois forces f1; f2 et son poids p telles que ces 3 forces fassent des angles non nuls entre elles ( utiliser deux fils pour f1 et f2) ; tracer les droites d'action de f1 et f2 matérialisées par les fils; le point d'intersection trouvé est le centre de gravité. tracer la verticale qui passe par ce point, c'est la droite d'action du poids. pour s'en assurer; elimer les deux fils et suspendre la plaque dans sans plan par un fil fixé au centre de gravité telle sorte que le fil tendu passe par la droite verticale déjà tracé

[Mathusalem]

Soit O un point d'un référentiel d'inertie situé hors du solide, et les points d'application des 3 forces.
Dès lors, les conditions pour un équilibre total sont


De (1), il vient que

En mettant dans (2)

[Mathusalem]

Je ne pense pas que la proposition soit vraie où alors ma définition de concourante est fausse.


Soit une poutre de longueur L
En 0, on applique une force F/2
En L, on applique une force F/2
En L/2, on applique une force -F



Le solide est en équilibre, vu de n'importe où.

En fait, je suis même assez tenté de dire la chose suivante :
Soit un point O d'un référentiel d'inertie à partir duquel les moments sont calculés.
telles que et , tel que . Sans avoir à forcément impliquer que les forces soit concourantes, sinon cela exclut tout couple parallèles.

EDIT: CE POST EST INUTILE

[Mathusalem]

C'est faux ce que je dis, deux droites parallèles sont concourrantes à l'infini.

Soit S le solide en question et P1, P2 deux points de ce solide, représentant les points d'applications de deux forces quelconques.
Soit O un point quelconque, pas forcément lié au solide.

1. Thm du centre de masse

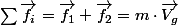
2. Thm du moment cinétique


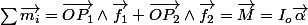
On cherche la force telle que



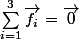
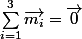
La première condition amène à

Ceci implique que est une combinaison linéaire des deux autres, et donc est coplanaire au plan crée par

Ceci montre déjà la coplanarité.
Afin de montrer le caractère concourrant, on peut faire les calculs brutaux et montrer. Néanmoins, voici une astuce:
Soit O' le point d'intersection des droites issues de
Alors, le thm. du moment cinétique livre


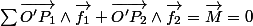
En effet, est colinéaire à et de même pour .
Ainsi, vu depuis O', la somme des moments est nulle.
Soit P3 le point d'application de , alors on veut



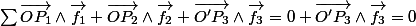
Ceci est vrai si
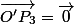- , i.e O' et P3 sont confondus
- est parallèle à
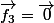- or ceci n'est en général pas satisfait puisque l'on ne suppose pas la somme des deux forces initiales comme nulle.

La deuxième condition implique, puisque O' est le point de croisement, que pointe vers le point de croisement, et donc les trois forces sont concourrantes.
La première implique la même chose de manière évidente.




Pour l'explication plus instinctive, vu que je sais pas le niveau que tu as :
Le théorème du moment cinétique caractérise ta vitesse de rotation pour des forces données. Celles-ci ne peuvent-être quelconques, elles doivent créer des moments de force pour ajouter de la rotation

Dans le cas d'une poutre, si je m'assieds au bord, cette force la fait tourner, si je pousse vers le centre de la poutre, elle se déplace (thm du centre de masse) mais elle ne tourne pas. Vu depuis le centre de la poutre, si je m'assieds, c'est une force tangentielle, et donc me fait tourner. Si je pousse, c'est une force radiale (vers le point d'observation) et ne fais pas tourner. La première crée un moment, la deuxième pas. Donc la première fait tourner, la deuxième pas. Enfait, le produit vectoriel travaille ici comme "sélécteur de forces" qui créent et ne créent pas de moments.

Cependant, qu'un solide ne tourne pas ne veut pas dire que le moment cinétique en un point O est nul. En effet, si je regarde un train qui me passe devant, le train ne tourne pas. Cependant, le système [moi - train] a une rotation, puisque moi, l'observateur, doit tourner ma tête pour suivre le train (très très qualitatif..)
Donc le moment cinétique et la variation du moment cinétique (a quel point on tourne de plus en plus vite/lentement) dépend du point O duquel on observe les choses.

L'astuce était de dire ici : Je me place dans un point tel que vu de ce point, il n'y a aucune rotation du solide. Ce point c'est le point d'intersection des droites issues des deux forces que j'ai posé. Une 3ème force qui aurait le bon goût de ne pas provoquer un moment de force doit directement pointer vers moi, le point d'intersection - ce qui montre la nature concourrante des forces. Ensuite, sa norme doit juste être telle qu'elle satisfasse le thm du centre de masse.

[fal]

dans votre exple:
Soit une poutre de longueur L
En 0, on applique une force F/2
En L, on applique une force F/2
En L/2, on applique une force -F
il fallait indiquer les directions et les sens; il manque le poids.
mais je comprends que les directions sont verticales avec le sens de f1 et f2 est l'opposé de f3/
il faut dire que ce ce vous dites est un cas particulier avecl les forces coliniaires. mais si les forces f1 et f2 ne sont pas coliniaires; on retrouve ce qu j'ai dit dans le 1 er message. et comme on le sait la physique nait de l'exprience; je vous le suggere.

[Mathusalem]

Dans mon exemple il ne manque pas le poids. Je suppose un problème avec 3 forces quelconques, l'une peut être le poids.
Les deux droites d'actions matérialisées par les fils de votre exemple ne s'intersectent pas au point de gravité.
Et pour finir, vous avez pris un cas particulier : un problème avec une plaque plane suspendue à deux fils soumise au poids. C'est très restrictif et n'explique pas pourquoi les 3 forces doivent être concourrantes.
J'ai, dans mon deuxième post, traité le cas général d'un solide S soumis à 3 forces. (et montré pourquoi elles sont concourrantes)