Accélération, et dérivées

par **variobike01** » 19 Mai 2009, 20:37

Bonsoir à tous.

J'ai quelques difficultés à comprendre comment on peut effectuer ce calcul :

=

.

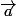
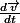
Je sais qu'il s'agit de la dérivée du vecteur vitesse par rapport au temps, mais je ne vois pas bien comment on peut dériver un vecteur vitesse... Car même en prenant la norme de ce vecteur on tomberais sur une constante donc sur 0 lors de la dérivation . :hein:
Pourriez vous alors m'expliquer un peu mieux cette notion qui est floue ?

Merci

++
Rémi

par **Dominique Lefebvre** » 19 Mai 2009, 21:24

Bonsoir,

Commençons par écrire les choses autrement.
Imaginons un mobile qui se déplace dans un référentiel Ox, avec un vecteur unitaire i.
L'abscisse du mobile est une fonction vectorielle du temps que je note x(t). je vais considérer que cette fonction est continue et 2 fois dérivable.
Par définition, la vitesse v du mobile est égale à v(t) = d(x(t))/dt . Si je projette sur Ox, j'ai v = d(x(t))/dt.
Toujours par définition, l'accélération a du mobile est égale à a(t) = d²(x(t))/dt², et donc a(t) = d(v(t))/dt.

Nota : j'applique la convention des physiciens : les vecteurs sont notés en gras.

par **le_fabien** » 20 Mai 2009, 06:33

Bonjour,
ou dit autrement, le vecteur accélération est défini par une variation de vecteur vitesse pendant une durée t.
Donc si le vecteur vitesse ne change pas pendant une certaine durée alors l'accélération est nulle.

par **variobike01** » 20 Mai 2009, 19:58

Merci pour vos réponses.
Il va falloir que je me fasse quelques exos la dessus ^^

Merci
++
Rémi

par **guigui51250** » 20 Mai 2009, 21:19

Bonjours,

Je profite de cette question pour poser la mienne ^^ en fait j'ai toujours eu du mal à comprendre la notion de vitesse instantannée... pour moi la vitesse instantannée c'est la vitesse à un instant t or à un instant, il ne peux pas y avoir de mouvement donc pas de vitesse puisque c'est juste un instant. Enfin voilà comment je raisonne.
Quelqu'un pourrai m'éclaircir un peu sur cette notion de vitesse instantannée svp?

Merci d'avance

Guillaume

par **Dominique Lefebvre** » 20 Mai 2009, 23:24

guigui51250 a écrit:Bonjours,

Je profite de cette question pour poser la mienne ^^ en fait j'ai toujours eu du mal à comprendre la notion de vitesse instantannée... pour moi la vitesse instantannée c'est la vitesse à un instant t or à un instant, il ne peux pas y avoir de mouvement donc pas de vitesse puisque c'est juste un instant. Enfin voilà comment je raisonne.
Quelqu'un pourrai m'éclaircir un peu sur cette notion de vitesse instantannée svp?

Merci d'avance

Guillaume

Bonsoir,
Tu sais sans doute c'est qu'est une dérivée en mathématique.... La notion de vitesse instantanée est très similaire. J'écris "très similaire" car les physiciens n'ont pas tout à fait la même notion que les mathématiciens d'un "infiniment petit" ou d'une élement différentiable. Mais peu importe! La vitesse instantanée est la dérivée temporelle de la fonction de mouvement. C'est une définition...
Et donc, dans ton approche, ce qui est inexact c'est "il ne peux pas y avoir de mouvement donc pas de vitesse puisque c'est juste un instant". Dans la définition de la vitesse instantanée, le "dt" ne représente pas un instant, mais un intervalle de temps entre deux instants, intervalle de temps que l'on peut choisir aussi petit que souhaité (car on suppose toujours, sans le dire, la fonction de mouvement comme continue et dérivable).

par **valentin.b** » 21 Mai 2009, 13:29

Bonjour,

Je pense que le terme vitesse instantannée est trompeur. On se pose effectivement les mêmes questions pour une dérivée en un point, il n'y a pas de dérivée sans continuité de la fonction que l'on dérive (on ne peut pas parler de dérivé un point). La dérivée en un point te donne des informations sur la fonction aux alentours de ce point, il n'y a pas de notion d'instantanné mais de proximité infinitésimale (que naturellement les physicien approximent comme instantannée).
Cela mène à la notion de développements limités, on peut localement décrire une fonction comme étant égale à sa tangente (le droite tangente, pas la fonction trigonométrique -_- ...), ce qui rejoint l'idée que la dérivée permet de décrire localement la fonction ...
(je me rend compte que j'ai plus ou moins dis la même chose ... désolé)

par **guigui51250** » 22 Mai 2009, 17:03

ok merci pour l'info, c'est vrai que le nom vitesse instantannée me perturbe un peu, la comparaison avec la dérivée en un point m'a permi de mieux comprend.
Merci

par **nuage** » 22 Mai 2009, 18:33

Salut,

guigui51250 a écrit:Bonjours,

Je profite de cette question pour poser la mienne ^^ en fait j'ai toujours eu du mal à comprendre la notion de vitesse instantannée... pour moi la vitesse instantannée c'est la vitesse à un instant t or à un instant, il ne peux pas y avoir de mouvement donc pas de vitesse puisque c'est juste un instant. Enfin voilà comment je raisonne.
Quelqu'un pourrai m'éclaircir un peu sur cette notion de vitesse instantannée svp?

Merci d'avance

Guillaume

je suppose que tu le sais, mais c'est un des paradoxes de Zénon d'Élée.
Et pas le moins amusant.

par **guigui51250** » 22 Mai 2009, 19:03

ah non je connaissais pas

^^

Accélération, et dérivées

Accélération, et dérivées

Qui est en ligne