(pour les figures géoplan me demander.) :id: :id:
Deux méthodes pour réussir à calculer le volume de ce cylindre :

où la surface en bleu est la surface du liquide de notre cylindre...
On sait déjà que ce volume est un prisme ayant un ménisque pour base.
Si on a en USI des valeurs connues : R le rayon,
L la longueur du cylindre
H la hauteur de liquide dans le cylindre depuis le fond de celui-ci
on a donc :
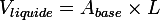
la difficulté résidant dans
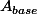
... :--:
Détermination de 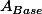 :1_ Avant la Terminale S : Géométriea : Quand le niveau est en dessous du milieu du cylindre
:1_ Avant la Terminale S : Géométriea : Quand le niveau est en dessous du milieu du cylindreC'est la méthode la plus longue. On considère le cercle qui est en fait la coupure du cylindre par un plan vertical :

On cherche à retrouver l'aire du ménisque formé par l'arc
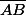
et le segment
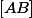
Or on retrouve ici un "camembert" d'angle

en °.
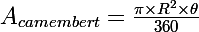
Retrouvons

par la géométrie : si on considère AOM rectangle en M, celui-ci étant le milieu de [AB] :
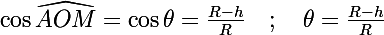
bon, nous avons donc l'aire du camembert, il faut maintenant soustraire l'aire du triangle (OAB) et le tour est joué!
} = frac{b\times h}{2})
Bon, sachant que (OAB) = 2(OAM), reste à calculer AM :
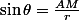
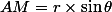
voilà! on réinjecte tout et ça donne une horrible formule énorme :
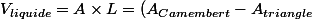\times L\\<br />V= (\frac{\pi R^2 \theta}{360}-\frac{2\times AM\times (r-h)}{2})\times L)
Je n'ai pas encore fini de tout réinjecter... reste AM et

:
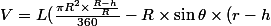))
en simplifiant et en remplaçant une bonne fois pour toutes :
^2}{R}))
OUFF, vive le copier/coller...
Quelqu'un est-il d'accord avec cette proposition? :help:
b) Quand le niveau se trouve au-dessus de la moitié du cylindreC'est en fait le même processus à l'envers cette fois, je ne vais donc pas vous faire l'affront de recommencer : :++:
) c) Quand le niveau est exactement à la moitié
c) Quand le niveau est exactement à la moitiéEh, oh, ça va là on se paie pas de ma tête?
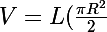)
c'est ça marrez-vous... :ptdr:
1_ Terminale S : IntégrationTout de suite ça devient plus simple... :we:
On va faire roter le cercle pour que ce soit plus lisible, et pour pouvoir faire des fonctions dans un repère orthonormé.
Soit le cercle trigo d'équation
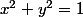
ou plutôt
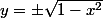
Notre cercle à nous est juste un agrandissement de celui-ci de facteur R. l'aire est donc multipliée par R²(à vos crayons...)
Ainsi on va trouver l'équivalent réduit de notre aire de ménisque sur le cercle trigo . Débarrassons-nous tout de suite du "plus ou moins" parce qu'en fait on trouve une symétrie d'axe (Ox) :
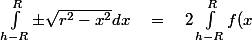dx)
Remis à l'échelle cu cercle trigo :
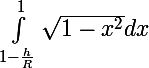
D'accord? ce ne sont que agrandissement/réductions.
Résolvons l'intégrale en remplaçant x par sin x (changement de variable)
^2}dx\quad = \quad \int_{1-\frac{h}{R}}^1 \cos x dx\\<br />= [\sin x]_{1-\frac{h}{R}}^1 = \sin 1 - \sin (1-\frac{h}{R}))
Ainsi on termine :
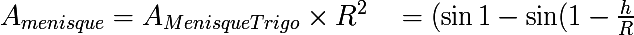)\times R^2)
Bon sur ce, je pense que j'ai assez bossé pour aujourd'hui, sachant qu'au départ ce n'était que pour graduer un balai qui mesure la jauge de fioul dans un réservoir... pfff...

Commentaires svp il doit forcément y a voir un problème...



