Bonjour à tous,
j'ai du mal à trouver la réponse à la question en gras.
Soit un triangle ABC
soit D tel que AD = 3AB
soit E tel que 2EA + EC = 0
Soit I et J milieux respectifs de [EB] et [CD]
2) J'ai prouvé que les points A,I et J sont alignés
3) 2EA + EC = 0
on a à la fin AE = 1/3 AC
On exprime AI et AJ en fonction non colinéaires AB et AC
AI = AB + BI par chasles
4) Exprimer AI en fonction de AB et AC
AI = 1/2AB+ 1/6AC
5) exprimer AJ en fonction de AB et AC
Merci par avance pour les personnes qui m'aideront
(Il n'y a pas de flèche qui indique le symbole de vecteurs car je ne sais pas comment l'écrire sur ordinateur)
Vecteurs
5 messages
- Page 1 sur 1
Re: vecteurs
Bonjour
Merci de nous le dire mais quand on écrit AD on va comprendre une mesure géométrique
si vous ne savez pas écrire un vecteur vous pouvez déclarer que v(AD) désigne un vecteur
et on déclare v(0) le vecteur nul
sinon pour info balises tex voir bouton
puis entre les deux balises \overrightarrow {AD}
pour le vecteur nul ce sera \overrightarrow {0}
Par ailleurs ABC est un triangle non plat
En effet dans l'énoncé il est dit que
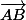 et
et 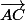 ne sont pas colinéaires
ne sont pas colinéaires
Par ailleurs ça serait bien de nous dire quelles sont les questions 1)2)3)
On les devine comment ces questions?
Je ne suis pas devin mais je vais faire semblant de l'être
יהוה אלהים est témoin que je n'ai pas le choix malgré qu'il m'interdit catégoriquement de faire cela
Il m'a certes autorisé à faire des tas de trucs genre boire et fumer parce que je suis un punk mais là c'est verboten de chez verboten
Donc du coup je refais l'énoncé avec les solutions des questions
Énoncé
Dans le plan affine muni de façon non canonique d'une structure d'espace vectoriel d'origine
(À noter qu'on est obligé ici de poser cela à cause des questions posées dans l'énoncé)
 un triangle non plat
un triangle non plat
(là encore on est obligé de le dire à cause des questions posées dans l'énoncé)
 un point tel que
un point tel que 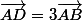
 un point tel que
un point tel que 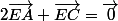
1)Exprimez les points et
et 
2)Soient le milieu de
le milieu de 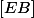 et
et  le milieu de
le milieu de 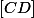
Montrer que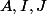 sont alignés
sont alignés
3)Même pharaon ne serait pas capable de deviner la question avec ses magiciens (et je ne suis pas Moïse)
4)Exprimer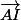 comme combinaison linéaire de
comme combinaison linéaire de 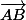 et
et 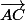
5)Exprimer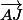 comme combinaison linéaire de
comme combinaison linéaire de 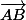 et
et 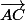
Solutions
1)
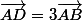
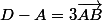
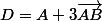
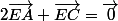
+C-E=O) l'origine
l'origine 
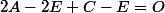 l'origine
l'origine 
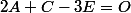 l'origine
l'origine 
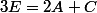
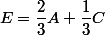
2)
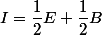
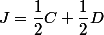
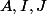 sont alignés revient à dire que
sont alignés revient à dire que 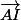 et
et 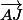 sont colinéaires
sont colinéaires
Pour montrer cela on va montrer qu'il existe un réel tel que
tel que 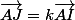
Pour cela on va considérer le point+\dfrac {1}{2}B-A)
On obtient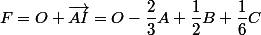
Pour cela on va considérer le point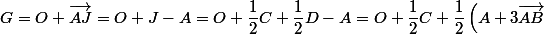-A)
On obtient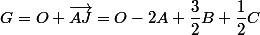
et donc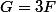 et donc
et donc 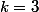 existe
existe
3) pas de question visible
4)on va poser
+b\left(C-A\right)=-\left(a+b\right)A+aB+bC=-\dfrac {2}{3}A+\dfrac {1}{2}B+\dfrac {1}{6}C)
donc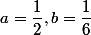 on vérifie
on vérifie 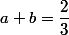
donc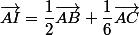
5)on va poser
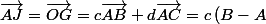+d\left(C-A\right)=-\left(c+d\right)A+cB+dC=-2A++\dfrac {3}{2}B+\dfrac {1}{2}C)
donc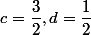 on vérifie
on vérifie 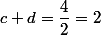
donc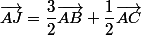
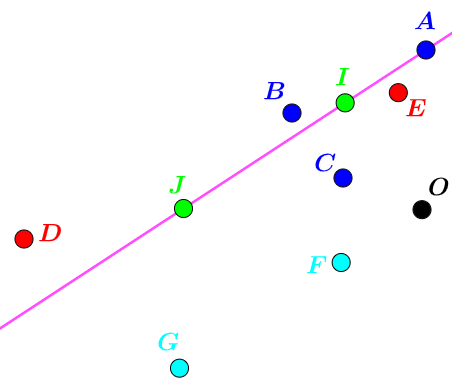
exemple
stephsay a écrit:Il n'y a pas de flèche qui indique le symbole de vecteurs car je ne sais pas comment l'écrire sur ordinateur
Merci de nous le dire mais quand on écrit AD on va comprendre une mesure géométrique
si vous ne savez pas écrire un vecteur vous pouvez déclarer que v(AD) désigne un vecteur
et on déclare v(0) le vecteur nul
sinon pour info balises tex voir bouton
puis entre les deux balises \overrightarrow {AD}
pour le vecteur nul ce sera \overrightarrow {0}
Par ailleurs ABC est un triangle non plat
En effet dans l'énoncé il est dit que
Par ailleurs ça serait bien de nous dire quelles sont les questions 1)2)3)
On les devine comment ces questions?
Je ne suis pas devin mais je vais faire semblant de l'être
יהוה אלהים est témoin que je n'ai pas le choix malgré qu'il m'interdit catégoriquement de faire cela
Il m'a certes autorisé à faire des tas de trucs genre boire et fumer parce que je suis un punk mais là c'est verboten de chez verboten
Donc du coup je refais l'énoncé avec les solutions des questions
Énoncé
Dans le plan affine muni de façon non canonique d'une structure d'espace vectoriel d'origine
(À noter qu'on est obligé ici de poser cela à cause des questions posées dans l'énoncé)
(là encore on est obligé de le dire à cause des questions posées dans l'énoncé)
1)Exprimez les points
2)Soient
Montrer que
3)Même pharaon ne serait pas capable de deviner la question avec ses magiciens (et je ne suis pas Moïse)
4)Exprimer
5)Exprimer
Solutions
1)
2)
Pour montrer cela on va montrer qu'il existe un réel
Pour cela on va considérer le point
On obtient
Pour cela on va considérer le point
On obtient
et donc
3) pas de question visible
4)on va poser
donc
donc
5)on va poser
donc
donc
exemple

Re: vecteurs
5)
On peut exprimer en fonction de
en fonction de  et
et 
Relation du milieu
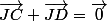
puis introduire
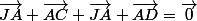
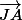 (ou
(ou 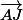 ) est le but donc on le laisse (même lettres)
) est le but donc on le laisse (même lettres)
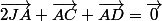
 est à garder, donc on garde, reste
est à garder, donc on garde, reste  à exprimer en fonction de
à exprimer en fonction de  et
et 
Or d'après énoncé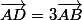
donc
)
edit: pour les flèches
tu peux écrire \vec{AB} et entourer par la balise [tex] [/ tex] (sans l'espace)
c'est un peu pénible au début mais ça aide grandement tes lecteurs qui saignent des yeux sinon
On peut exprimer
Relation du milieu
puis introduire
Or d'après énoncé
donc
edit: pour les flèches
tu peux écrire \vec{AB} et entourer par la balise [tex] [/ tex] (sans l'espace)
c'est un peu pénible au début mais ça aide grandement tes lecteurs qui saignent des yeux sinon
la vie est une fête 
Re: vecteurs
fatal_error a écrit: tu peux écrire \vec{AB}
Ah oui ok ça marche aussi
Du coup moi je me suis emmerdé en écrivant \overrightarrow {AD} pour rien alors
Merci Fatal_Error
Re: vecteurs
On remarquera aussi que (BE) et (CD) sont parallèles
En recopiant l'exo j'ai placé ça en question 3 vu que je ne vois pas quelle est cette question 3
En recopiant l'exo j'ai placé ça en question 3 vu que je ne vois pas quelle est cette question 3
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 78 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
