Vecteurs
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
eau-minérale
- Membre Relatif
- Messages: 139
- Enregistré le: 19 Sep 2006, 15:54
-
 par eau-minérale » 01 Nov 2006, 16:11
par eau-minérale » 01 Nov 2006, 16:11
Bonjour je n'arrive pas a trouvé le 2)
Soit ABC un triangle équilatéral de coté a et A' le symétrique de A par rapport à la droite (BC).
1) Calculer vAB . vAC en fonction de a (j'ai trouvé : a²/2)
2) Démontrer que pour tout point M du plan :
vMB . vMC = MA² + vMA . vAA' + (a²/2)
v signifie vecteur
Merci de votre aide
-
eau-minérale
- Membre Relatif
- Messages: 139
- Enregistré le: 19 Sep 2006, 15:54
-
 par eau-minérale » 01 Nov 2006, 16:28
par eau-minérale » 01 Nov 2006, 16:28
Est ce que quelqu'un pourrait m'aider s'il vous plait.
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 01 Nov 2006, 17:02
par Imod » 01 Nov 2006, 17:02
Introduis le point A dans MB et MC avec la relation de Chasles .
Imod
-
eau-minérale
- Membre Relatif
- Messages: 139
- Enregistré le: 19 Sep 2006, 15:54
-
 par eau-minérale » 01 Nov 2006, 18:15
par eau-minérale » 01 Nov 2006, 18:15
Merci de m'avoir répondu
Si je fais la relation de Chasle cela fait :
vMB . vMC = (vMA + vAB) . (vMA + v AC) = vMA . (vAB + vAC)
= vMA . (2a)
mais après ...
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 01 Nov 2006, 18:23
par Imod » 01 Nov 2006, 18:23
eau-minérale a écrit:vMB . vMC = (vMA + vAB) . (vMA + v AC) = vMA . (vAB + vAC)
= vMA . (2a)
??????????????????????????
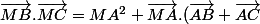+\vec{AB}.\vec{AC}=...)
.
Imod
-
eau-minérale
- Membre Relatif
- Messages: 139
- Enregistré le: 19 Sep 2006, 15:54
-
 par eau-minérale » 01 Nov 2006, 18:39
par eau-minérale » 01 Nov 2006, 18:39
Ah y fallait remplacer AA' par AB + AC j'y avait pas penser !
Mais je comprend pas pour prouver que de truc sont égaux il faut bien faire l'un moins l'autre = 0
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 01 Nov 2006, 18:48
par Imod » 01 Nov 2006, 18:48
eau-minérale a écrit:Mais je comprend pas pour prouver que de truc sont égaux il faut bien faire l'un moins l'autre = 0
Tu peux aussi continuer le calcul pour obtenir le second membre que tu veux .
Imod
-
eau-minérale
- Membre Relatif
- Messages: 139
- Enregistré le: 19 Sep 2006, 15:54
-
 par eau-minérale » 01 Nov 2006, 18:50
par eau-minérale » 01 Nov 2006, 18:50
Oui je sais mais la je vois pas comment faire
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 01 Nov 2006, 18:53
par Imod » 01 Nov 2006, 18:53
Tu peux par exemple introduire A' dans
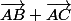
pour voir ce qui se passe .
Imod
-
eau-minérale
- Membre Relatif
- Messages: 139
- Enregistré le: 19 Sep 2006, 15:54
-
 par eau-minérale » 01 Nov 2006, 18:58
par eau-minérale » 01 Nov 2006, 18:58
Tu peux me montrer le début car la j'essaye toute les possibilités mais j'aimerais bien savoir où je vais.
-
eau-minérale
- Membre Relatif
- Messages: 139
- Enregistré le: 19 Sep 2006, 15:54
-
 par eau-minérale » 01 Nov 2006, 19:01
par eau-minérale » 01 Nov 2006, 19:01
ACA'B est un losange donc vAB=vCA'
vMB.vMC=(vMA+vAB)(vMA+vAC)=MA²+vAB.vMA+vMA.vAC+vAB.vAC=MA²+vMA(vAB+vAC)+a²/2=MA²+vMA(vCA'+vAC)+a²/2=MA²+vMA.vAA'+a²/2
-
Imod
- Habitué(e)
- Messages: 6483
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 01 Nov 2006, 19:08
par Imod » 01 Nov 2006, 19:08

et on regarde ton dessin et on essaie de conclure , en math on n'a rien sans efforts .
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
