Vecteurs.

par **Florent9819** » 21 Fév 2015, 19:02

Bonsoir , voila je rencontre un petit problème mathématique lors d'un devoirs voici lénoncé

Points A(1;1) , B(2;3), C(-1,;0)

Détermine un point D pour que : a) ABCD soit un parallélogramme
b) ACDB soit un parallélogramme

Je ne sais pas du tout par ou commencer j'ai placé mes points dans un repère orthonormée pour m'aider visuellement mais je n'arrive pas a commencer

Merci à ceux qui m'aideront

par **XENSECP** » 21 Fév 2015, 19:13

Salut,

Parallélogramme = côtés opposés parallèles ce qui se traduit par vecteurs colinéaires. Et même plus: vecteurs égaux !

Pour le premier tu dois donc trouver D(a,b) tel que:

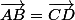
ET

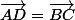
2 inconnues (a et b), 2 équations: à toi de jouer

par **Florent9819** » 21 Fév 2015, 19:48

Donc je dois calculer les composantes de AB et BC et comme il sont opposé je dois opposé les vecteur AB et BC donc on trouvera les composantes de CD ET AD et je n'ai plus qu'a décomposer pour trouver les différents ( ; ) ?

par **siger** » 21 Fév 2015, 20:01

bonjour

ce que tu ecris est difficilement comprehensible!
parallelogramme ABCD: les cotes AB et CD sont egaux et paralleles, donc en vecteurs on a
AB = DC pour tenir compte du sens des vecteurs
ce qui se traduit par
xB -xA = xD -xC d'ou xD = ..
meme chose pour yD...

meme raisonnement pour la question b/ avec un parallelogramme different, d'ou une egalite vectorielle differente.......

par **Florent9819** » 21 Fév 2015, 20:14

D'accord désolé je m'exprime mal mais c'est à peu près ce que je voulais dire sauf que moi je prenais les deux vecteur ( donc AB = DC et je prenais aussi l'autre vecteur CB = DA ) donc j'avais une inégalité soit merci ! :)

J'ai un autre problème ( mon travail est sur les vecteurs donc je poste ici )

J'ai A(K;1) B(6;7) mais je dois trouver K en sachant que la norme de AB = ;)37.

Je me suis dit que c'était une équation donc j'ai fait :

;)(6-K)²+(7-1)² = ;)37

mais c'est impossible de faire sortir le K non ?

par **siger** » 22 Fév 2015, 09:46

re

parallelogramme ABCD
en vecteurs AB=DC suffit' car cela entraine BC=AD....

ecris AB^2 = 37
d'ou une equation du second degre en K
A est sur une parallele a Ox d'equation y= 1
il y a donc deux points A symetriques par rapport a xB= 6 ( donc deux valeurs de k) qui correspondent a AB^2= 37

Vecteurs.

Vecteurs.

Qui est en ligne