Bonjour à tous, je suis bloquée à un problème de vecteurs qui est le suivant:
O centre du cercle (C) de rayon 1
point M' défini par: Vect(MM')=Vect(MA)+Vect(MB)+2Vect(MC)
point G: Vect(GA)+Vect(GB)+2Vect(GC)=0
point O': Vect(GO')= - 3Vect(GO)
déterminer une relation entre Vect(O'M') et Vect(OM)
J'ai pour le moment fait:
MM'=MA+MB+2MC
MM'=MG+GA+MG+GB+2(MG+GC)
MM'=4MG+GA+GB+2GC
MM'=4MG+0
je ne sais pas comment aboutir avec ça
Toute aide est la bienvenue!
VECTEURS CHASLES...
5 messages
- Page 1 sur 1
Re: VECTEURS CHASLES...
Bonjour,
tu ne nous dis pas à quoi sert ton cercle, ni où sont les points A,B,C,O', etc. Je crois qu'il nous manque des données pour pouvoir te répondre.
tu ne nous dis pas à quoi sert ton cercle, ni où sont les points A,B,C,O', etc. Je crois qu'il nous manque des données pour pouvoir te répondre.
Re: VECTEURS CHASLES...
Salut Mannnon,
partons de ce que l'on cherche!
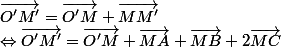
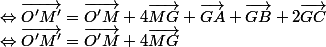
(ce que tu avais calculé pour MM' était juste)
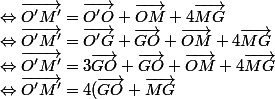 +\vec{OM} \\ \Leftrightarrow \vec{O'M'}= -3\vec{OM})
partons de ce que l'on cherche!
(ce que tu avais calculé pour MM' était juste)
Modifié en dernier par liryck le 23 Fév 2017, 23:13, modifié 1 fois.
Re: VECTEURS CHASLES...
bonsoir
attention de ne pas oublier la question en faisant des calculs ......
montrer que MM' = 4 MG , c'est bien mais ça ne fait pas avancer le schmilblik !
O'M' = O'G + GO + OM +MM'
= 3GO + GO + OM+ 4MG
= 4(MG+GO) + OM
= 4(MO) + OM
=. ......
attention de ne pas oublier la question en faisant des calculs ......
montrer que MM' = 4 MG , c'est bien mais ça ne fait pas avancer le schmilblik !
O'M' = O'G + GO + OM +MM'
= 3GO + GO + OM+ 4MG
= 4(MG+GO) + OM
= 4(MO) + OM
=. ......
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
