Vecteur

[girl2067]

Bonjour je rencontre qlqs difficultés pour un exercice de maths dont voici l'enoncé si je pourrais avoir qlqs indications cela ne serait pas de refus !!!
merci d'avance

OIKJ est un carré, A est un point de la droite (OI) et B un point de la droite (OJ) passant par A coupe (JK) en A', et la parallèle à (OI) passant pas B coupe (IK) en B'.

Le but de cet exercice est de démontrer que les droites (AB'),(A'B) et (OK) sont parallèle ou concourantes.

Pour cela, on munit la plan du repère (O;vecteur OI; vecteur OJ)
1)a) Justfier l'existence de deux points a et b tels que: /vec{OA}=a /vec{OI} et /vec{OB}=b /vec{OJ}
b)Donner les coordonnées des points A,A',B,B' et K.
c)Exprimer en fonction de a et b les coordonnées des vecteurs AB',BA' et OK .

2)a) Montrer que "(AB')et (A'B) parallèles" équivaut à "a+b=1" et qu'alors (AB') et (A'B) sont parallèles à (OK).
b) Faire une figure illustrant la situation précédente en précisant les valeurs de a et de b choisies.

3)a)Trouver une équation cartésienne des droites (OK), (A'B) et (AB').
b) On suppose que (AB') et (A'B) sont sécantes en P.
Prouver que P est sur (OK)."

Voici le lien de la figure fourni avec l'exercice : http://img90.imageshack.us/img90/2682/forum1234201xh7.jpg

[girl2067]

personne ne peut m'aider ou koi???????????????,

[armor92]

Bonsoir,

Pour cela, on munit la plan du repère (O;vecteur OI; vecteur OJ)
1)a) Justfier l'existence de deux points a et b tels que: /vec{OA}=a /vec{OI} et /vec{OB}=b /vec{OJ}

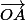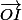A est sur la droite OI, ca veut dire que les vecteurs et sont colinéaires.
Il existe un réel a tel que

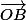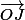De même B est sur la droite OJ, et sont colinéaires.
Il existe un réel b tel que

b)Donner les coordonnées des points A,A',B,B' et K.

Dans le repère (O;vecteur OI; vecteur OJ)
A a pour coordonnées (a,0)
B a pour coordonnées (0,b)


Donc A' a pour coordonnées (a,1)


Donc B' a pour coordonnées (1,b)


Donc K a pour coordonnées (1,1)

c)Exprimer en fonction de a et b les coordonnées des vecteurs AB', BA' et OK .

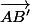a pour composantes (1 - a, b) dans le repère


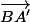a pour composantes (a, 1 - b) dans le repère


Donc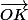 a pour coordonnées (1,1) dans le repère

[armor92]

2)a) Montrer que "(AB')et (A'B) parallèles" équivaut à "a+b=1" et qu'alors (AB') et (A'B) sont parallèles à (OK).

"(AB')et (A'B) parallèles" équivaut à et colinéaires
La colinéarité des deux vecteurs peut s'exprimer par déterminant() = 0
déterminant() = (1-a)(1-b) - ab = 1 - a - b
Donc on doit avoir : a + b = 1

Si on suppose qu'on a cette condition, on peut montrer que colinéaire à et

En effet, a pour composantes (1 - a, 1 - a) et a pour composantes (a, a)
On a donc : et

colinéaire à et donc (OK) parallèle à (AB') et (BA')

3)a)Trouver une équation cartésienne des droites (OK), (A'B) et (AB').

Equation cartésienne de (Ok) : y=x

Pour trouver l'equation cartésienne de (A'B), on exprime que M appartient à la droite (A'B) si et seulement si est colinéaire à , c'est à dire déterminant() = 0
déterminant() = a * (y - b) -(1 - b) * x = 0
Equation cartésienne de (BA') : (b - 1) * x + a * y = a * b

Pour trouver l'equation cartésienne de (AB'), on exprime que M appartient à la droite (AB') si et seulement si est colinéaire à , c'est à dire déterminant() = 0
déterminant() = (1 - a) * y - b * (x - a) = 0
Equation cartésienne de (AB') : b * x + (a - 1) * y = a * b

b) On suppose que (AB') et (A'B) sont sécantes en P.
Prouver que P est sur (OK)."

Le point P(x,y) satisfait en même temps aux équations de (BA') et (AB')
(b - 1) * x + a * y = a * b (1)
b * x + (a - 1) * y = a * b (2)

(2) - (1) donne : x - y = 0 donc x = y
Donc P est sur la droite (OK)

[girl2067]

merci bcp je regarde cela dans la semaine avec une amie, j'ai aussi un dm de physique à faire, si j'ai des questions pourrais-je vous en faire part ????
merci d'avance
bye