Bonsoir tout le monde,
J'ai trouvé un exercice assez dure, j'ai répondue à la plupart des questions, j'aimerais qu'on vérifie mes réponses, merci de votre aide.
Je ne peux pas écrire l'exo puisqu'il y a des signes de vecteurs, ils ne sont pas disponible ici.
Vecteur exercice d'entraînement.
6 messages
- Page 1 sur 1
Re: Vecteur exercice d'entraînement.
Salut,
guide-utilisation-f41/ecrire-des-belles-formules-mathematiques-balises-tex-t70548.html
Par exemple \vec{AB} entre balises tex ->
guide-utilisation-f41/ecrire-des-belles-formules-mathematiques-balises-tex-t70548.html
Par exemple \vec{AB} entre balises tex ->
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Vecteur exercice d'entraînement.
Je te remercie ! Je vais m'y coller pour rédiger mon exercice alors !
Re: Vecteur exercice d'entraînement.
1) ABCD est un rectangle de centre I.
a) Construire le représentant d'origine C du vecteur \vec{u} = \vec{AB}+ \vec{CI}+ \vec{BC}.
b) A quel vecteur de la figure, le vecteur \vec{U} semble t'il égal ?
Prouver cette conjecture.
2)ABCD est un parallélogramme. E et F sont tel que \vec{DE}=2/3 \vec{DB} et \vec{DF}=1/3 \vec{BD}.
G et H sont les points tels que ABGE et ABHF sont deux parallélogrammes.
a) Faire une figure.
b) Démontrer que les points G,C et H sont alignés.
Voilà mes réponses :
1)a) Construction de la figure faites.
1)b)\vec{AI}
\vec{U}=\vec{AB}+\vec{CI}+\vec{BC}.
\vec{U}=\vec{AC}+\vec{CI}.
\vec{U}+\vec{AI}.
2)a)Construction de la figure faites.
2)b)Comment démontrer qu'ils sont alignés, je sais que lorsque deux trois (exemple : AB et AI) sont colinéaires donc AB//AI, alors elles sont colinéaires, elle possède le points en commun A, alors en peux affirmez qu'elle sont alignés c'est deux droites.
a) Construire le représentant d'origine C du vecteur \vec{u} = \vec{AB}+ \vec{CI}+ \vec{BC}.
b) A quel vecteur de la figure, le vecteur \vec{U} semble t'il égal ?
Prouver cette conjecture.
2)ABCD est un parallélogramme. E et F sont tel que \vec{DE}=2/3 \vec{DB} et \vec{DF}=1/3 \vec{BD}.
G et H sont les points tels que ABGE et ABHF sont deux parallélogrammes.
a) Faire une figure.
b) Démontrer que les points G,C et H sont alignés.
Voilà mes réponses :
1)a) Construction de la figure faites.
1)b)\vec{AI}
\vec{U}=\vec{AB}+\vec{CI}+\vec{BC}.
\vec{U}=\vec{AC}+\vec{CI}.
\vec{U}+\vec{AI}.
2)a)Construction de la figure faites.
2)b)Comment démontrer qu'ils sont alignés, je sais que lorsque deux trois (exemple : AB et AI) sont colinéaires donc AB//AI, alors elles sont colinéaires, elle possède le points en commun A, alors en peux affirmez qu'elle sont alignés c'est deux droites.
Re: Vecteur exercice d'entraînement.
Le but dans ce type de question, c'est de "remonter" petit à petit toutes les construction de façon à ne faire apparaitre QUE les points de départ, voire même uniquement certains d'entre eux.
Par exemple ici, on peut exprimer tout les vecteurs à l'aide uniquement de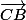 et
et 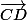 et si on exprime à la fois
et si on exprime à la fois 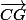 et
et 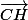 à l'aide de ces vecteurs, on devrait voir s'ils sont colinéaires ou pas.
à l'aide de ces vecteurs, on devrait voir s'ils sont colinéaires ou pas.
Je te le fait pour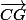 .
.
Le point C est un point "de base" donc pas de soucis. Concernant G, ce qu'on sait, c'est que ABGE est un parallélogramme et donc, concernant G, que et que
et que  . Pour faire "disparaitre" G, il faut utiliser une des deux relation (à priori, n'importe laquelle) donc on écrit par exemple :
. Pour faire "disparaitre" G, il faut utiliser une des deux relation (à priori, n'importe laquelle) donc on écrit par exemple :

Le vecteur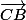 , c'est nickel, c'est un des vecteur "de base", par contre il faut simplifier l'autre et là, il y a pas le choix vu que la seule chose qu'on sait concernant E, c'est que
, c'est nickel, c'est un des vecteur "de base", par contre il faut simplifier l'autre et là, il y a pas le choix vu que la seule chose qu'on sait concernant E, c'est que  ce qui conduit à écrire que :
ce qui conduit à écrire que :
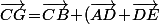\!=\!\vec{CB}\!+\!\vec{AD}\!+\!\frac{2}{3}\vec{DB})
Dans y'a pas de C, mais vu que ABCD est un parallélogramme on a
y'a pas de C, mais vu que ABCD est un parallélogramme on a  et concernant
et concernant 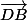 , y'a qu'à introduire le point C :
, y'a qu'à introduire le point C :
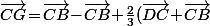}\!=\!\frac{2}{3}\vec{CB}\!-\!\frac{2}{3}\vec{CD})
Il y a évidement plus rapide (*), mais là, ça a le bon gout de se faire sans réfléchir et c'est un très bon entrainement concernant la manipulation des vecteurs donc je t'inciterais fortement à faire la même chose en partant de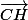 .
.
(*) si on regarde bien les calculs çi dessus, ben en fait on a très rapidement montré que donc il suffirait de montrer que
donc il suffirait de montrer que 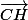 est lui aussi colinéaire à
est lui aussi colinéaire à 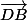 pour conclure.
pour conclure.
Par exemple ici, on peut exprimer tout les vecteurs à l'aide uniquement de
Je te le fait pour
Le point C est un point "de base" donc pas de soucis. Concernant G, ce qu'on sait, c'est que ABGE est un parallélogramme et donc, concernant G, que
Le vecteur
Dans
Il y a évidement plus rapide (*), mais là, ça a le bon gout de se faire sans réfléchir et c'est un très bon entrainement concernant la manipulation des vecteurs donc je t'inciterais fortement à faire la même chose en partant de
(*) si on regarde bien les calculs çi dessus, ben en fait on a très rapidement montré que
Modifié en dernier par Ben314 le 02 Jan 2017, 21:41, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Vecteur exercice d'entraînement.
Bizarrement, en classe nous n'avons pas vus ce type de démonstration, en lisant tes explications qui ont l'air logique, je peine à comprendre
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
