Variations d'une suite
16 messages
- Page 1 sur 1
Variations d'une suite
Bonjour tout le monde
Je viens de rentrer en terminale S cette année et premier cours c'est des révisions sur les suites de l'année passé cependant il y a quelque chose que je ne comprends pas !
Pour déterminer le sens de variation d'une suite on peut faire :
Un+1-Un
Un=f(n)
ou comparer Un+1/Un a 1
je connais les trois méthode le problème est que je ne comprends pas quand il faut faire Un+1 - Un et quand il faut faire Un+1/Un et comparer le résultat a 1 , je ne vois pas a quel moment il faut utiliser telle méthode , est ce que les deux méthodes marchent dans tout les cas ou bien y a t'il des conditions a respecter qui diffèrent entre ces deux méthodes ?
Merci d'avance :)
Je viens de rentrer en terminale S cette année et premier cours c'est des révisions sur les suites de l'année passé cependant il y a quelque chose que je ne comprends pas !
Pour déterminer le sens de variation d'une suite on peut faire :
Un+1-Un
Un=f(n)
ou comparer Un+1/Un a 1
je connais les trois méthode le problème est que je ne comprends pas quand il faut faire Un+1 - Un et quand il faut faire Un+1/Un et comparer le résultat a 1 , je ne vois pas a quel moment il faut utiliser telle méthode , est ce que les deux méthodes marchent dans tout les cas ou bien y a t'il des conditions a respecter qui diffèrent entre ces deux méthodes ?
Merci d'avance :)
Bonjour,
En fait, cela se devine suivant la forme de la suite. Très souvent si tu as une suite de la forme an + b (ce n'est qu'un exemple) alors il faudra utiliser un+1 - un.
Si au contraire tu as une suite de la forme (an + b) / (cn + d) (par exemple) alors il faudra passer plutôt par un+1 / un.
Entraine toi et tu verras que rapidement tu pourras deviner quelle méthode utilisée.
En fait, cela se devine suivant la forme de la suite. Très souvent si tu as une suite de la forme an + b (ce n'est qu'un exemple) alors il faudra utiliser un+1 - un.
Si au contraire tu as une suite de la forme (an + b) / (cn + d) (par exemple) alors il faudra passer plutôt par un+1 / un.
Entraine toi et tu verras que rapidement tu pourras deviner quelle méthode utilisée.
Quand tu as explicitement Un=f(n), il est presque toujours plus simple d'étudier la fonction f(x) (en la dérivant, etc ...) sauf si la fonction est vraiment compliquée (avec des factorielles ou des valeurs absolues rendant difficile la dérivation).
Quand on te donne la suite sous forme récurrente ou bien si l'expression est compliquée alors il faut regarder la structure de l'expression. S'il y a des multiplications, on va plutôt prendre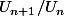
exemple Un=2^n/n! ou
S'il y a des additions alors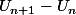 est souvent mieux adapté
est souvent mieux adapté
exemple Un=n²-n ou
Bon, mais c'est surtout une question de feeling, il n'y a pas de règle absolue.
Quand on te donne la suite sous forme récurrente ou bien si l'expression est compliquée alors il faut regarder la structure de l'expression. S'il y a des multiplications, on va plutôt prendre
exemple Un=2^n/n! ou
S'il y a des additions alors
exemple Un=n²-n ou
Bon, mais c'est surtout une question de feeling, il n'y a pas de règle absolue.
warsoling a écrit:Bonjour tout le monde
Je viens de rentrer en terminale S cette année et premier cours c'est des révisions sur les suites de l'année passé cependant il y a quelque chose que je ne comprends pas !
Pour déterminer le sens de variation d'une suite on peut faire :
Un+1-Un
Un=f(n)
ou comparer Un+1/Un a 1
je connais les trois méthode le problème est que je ne comprends pas quand il faut faire Un+1 - Un et quand il faut faire Un+1/Un et comparer le résultat a 1 , je ne vois pas a quel moment il faut utiliser telle méthode , est ce que les deux méthodes marchent dans tout les cas ou bien y a t'il des conditions a respecter qui diffèrent entre ces deux méthodes ?
Merci d'avance
salut
u(n+1) - u(n) ... est la définition pour les variations d'une suite ...
trois outils pour atteindre un même résultat ... mais lequel utiliser ? ....
il suffit de savoir lire et calculer pour choisir "la méthode optimale" (la plus efficace) ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:salut
u(n+1) - u(n) ... est la définition pour les variations d'une suite ...
trois outils pour atteindre un même résultat ... mais lequel utiliser ? ....
il suffit de savoir lire et calculer pour choisir "la méthode optimale" (la plus efficace) ....
Ok dac merci mais mis à part l'optimalité de la méthode par rapport à la suite il n'y a aucune contrainte qui nous empêche d'utiliser l'une ou l'autre ?
warsoling a écrit:Ok dac merci mais mis à part l'optimalité de la méthode par rapport à la suite il n'y a aucune contrainte qui nous empêche d'utiliser l'une ou l'autre ?
la comparaison du quotient à 1 est utilisé pour des termes positifs d'une part et d'autre part le quotient est compatible avec le produit donc regarder l'expression de u(n)
la soustraction étant compatible avec l'addition là encore est plus intéressante si l'expression de u(n) est sous forme d'une somme ....
quant à u(n) = f(n) à nouveau bien pratique si les variations de f sont simples à déterminer ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:la comparaison du quotient à 1 est utilisé pour des termes positifs d'une part et d'autre part le quotient est compatible avec le produit donc regarder l'expression de u(n)
la soustraction étant compatible avec l'addition là encore est plus intéressante si l'expression de u(n) est sous forme d'une somme ....
quant à u(n) = f(n) à nouveau bien pratique si les variations de f sont simples à déterminer ....
D'accord merci beaucoup à tous j'ai compris la
Excuser moi de vous enquiquiner mais je ne cerne vraiment pas O_o
warsoling a écrit:D'accord merci beaucoup à tous j'ai compris laD'ailleurs en parlant de Un=F(n) il y a un exercice ou on doit déterminer les variations de Un= 5n^2-20n-6 moi je pensais donc faire f(x)=5x^2-20x-6 pour trouver les variations de la fonction et donc de la suite mais finalement je vois sur la correction que la prof a dérivé la fonction pour obtenir 10x-20 et finalement déduire que la suite est croissante a partir de n>2 , je ne comprends pas pourquoi elle a utiliser la dérivé et n'utilise pas les variations de la fonction tout simplement ?
Excuser moi de vous enquiquiner mais je ne cerne vraiment pas O_o
ben il faut bien les connaître les variations de la fonction !!!!
la dérivée est un outil pour les obtenir ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
