Variations de F et √f
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Apritzz
- Messages: 6
- Enregistré le: 09 Nov 2013, 14:23
-
 par Apritzz » 09 Nov 2013, 14:31
par Apritzz » 09 Nov 2013, 14:31
Salut tout le monde , j'aurai besoin d'aide pour un exercice car je bloque complètement :/ Alors que normalement je l'ai réussis plutôt bien ces types d'exercices ..
Donc on nous dit , f est la fonction définie sur R par f(x) = x² - 2x + 3
1. Dressez le tableau de variation de f .
2. a) Pourquoi la fonction g : x --> ;)f(x) est-elle définie pour tout nombre de R ?
b) Dressez le tableau de variation de g.
c) Si x appartient à l'intervalle [0 ; 2] , à quel intervalle appartient g(x) ?
Je remercie ceux qui pourraient m'aider :)
& si c'est pas le cas , c'est pas grave ;)
-
Frednight
- Membre Rationnel
- Messages: 616
- Enregistré le: 04 Fév 2007, 17:03
-
 par Frednight » 09 Nov 2013, 15:16
par Frednight » 09 Nov 2013, 15:16
Apritzz a écrit:2. a) Pourquoi la fonction g : x -->

f(x) est-elle définie pour tout nombre de R ?
la fonction
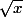
est définie sur quel intervalle?
-
Apritzz
- Messages: 6
- Enregistré le: 09 Nov 2013, 14:23
-
 par Apritzz » 09 Nov 2013, 16:20
par Apritzz » 09 Nov 2013, 16:20
Frednight a écrit:la fonction
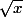
est définie sur quel intervalle?
Il n'y aucune indication supplémentaire a mon énoncer , je pourrais pas te répondre :/
-
Frednight
- Membre Rationnel
- Messages: 616
- Enregistré le: 04 Fév 2007, 17:03
-
 par Frednight » 09 Nov 2013, 16:31
par Frednight » 09 Nov 2013, 16:31
je ne te parle pas de ce qui est marqué dans ton énoncé mais plutôt ce qu'il y a dans ton cours :lol3:
-
Apritzz
- Messages: 6
- Enregistré le: 09 Nov 2013, 14:23
-
 par Apritzz » 09 Nov 2013, 21:10
par Apritzz » 09 Nov 2013, 21:10
Frednight a écrit:je ne te parle pas de ce qui est marqué dans ton énoncé mais plutôt ce qu'il y a dans ton cours :lol3:
Elle est défini sur l'intervalle [0 ; + infini [ :lol3:
-
Frednight
- Membre Rationnel
- Messages: 616
- Enregistré le: 04 Fév 2007, 17:03
-
 par Frednight » 09 Nov 2013, 21:26
par Frednight » 09 Nov 2013, 21:26
Apritzz a écrit:Elle est défini sur l'intervalle [0 ; + infini [ :lol3:
Très bien
et compte tenu de cela, à quel intervalle doit appartenir
)
pour que
})
soit définie?
-
Apritzz
- Messages: 6
- Enregistré le: 09 Nov 2013, 14:23
-
 par Apritzz » 10 Nov 2013, 09:03
par Apritzz » 10 Nov 2013, 09:03
Frednight a écrit:Très bien
et compte tenu de cela, à quel intervalle doit appartenir
)
pour que
})
soit définie?
Ce n'est pas clairement formuler mais f(x) doit appartenir a [0 ; +infini [ (je pense)
-
Frednight
- Membre Rationnel
- Messages: 616
- Enregistré le: 04 Fév 2007, 17:03
-
 par Frednight » 10 Nov 2013, 09:10
par Frednight » 10 Nov 2013, 09:10
oui c'est ça
et pour quels

)
est-elle positive?
-
Apritzz
- Messages: 6
- Enregistré le: 09 Nov 2013, 14:23
-
 par Apritzz » 10 Nov 2013, 11:19
par Apritzz » 10 Nov 2013, 11:19
Frednight a écrit:oui c'est ça
et pour quels

)
est-elle positive?
Pour tout x réel positif ?
-
Frednight
- Membre Rationnel
- Messages: 616
- Enregistré le: 04 Fév 2007, 17:03
-
 par Frednight » 10 Nov 2013, 11:47
par Frednight » 10 Nov 2013, 11:47
c'est ça mais tu dois le démontrer
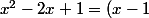^2)
(identité remarquable)
qu'est-ce que cela implique au niveau du signe de ce polynôme?
-
Apritzz
- Messages: 6
- Enregistré le: 09 Nov 2013, 14:23
-
 par Apritzz » 10 Nov 2013, 14:51
par Apritzz » 10 Nov 2013, 14:51
Frednight a écrit:c'est ça mais tu dois le démontrer
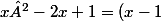^2)
(identité remarquable)
qu'est-ce que cela implique au niveau du signe de ce polynôme?
Dans mon cours pour démontrer que f est strictement croissante sur [0 ; +infini [ , On pose A = Delta y / Delta x pour trouver au final 1 /

b +

A qui prouve que A > 0
-
Frednight
- Membre Rationnel
- Messages: 616
- Enregistré le: 04 Fév 2007, 17:03
-
 par Frednight » 10 Nov 2013, 14:56
par Frednight » 10 Nov 2013, 14:56
Frednight a écrit:c'est ça mais tu dois le démontrer
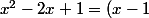^2)
(identité remarquable)
qu'est-ce que cela implique au niveau du signe de ce polynôme?
je ne t'ai pas demandé quel était son sens de variation mais bien son SIGNE (positive ou négative).
je te fais au passage remarquer que l'expression que j'ai marquée est égale au
carré de
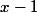
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
(identité remarquable)
(identité remarquable)
