Variation suite récurrente 1ère S

[nan]

Bonjour,
Je coince complètement sur les variations de la suite récurrente suivante:
U indice (n+1)=racine((U indice n) au carré + 6)
Je dois pour cela faire la soustraction de U indice n+1 - U indice n pour étudier les variations.
Le souci, c'est que je ne vois pas ce que je peux faire avec les racines qui possèdent une addition à l'intérieur de chacune.

Auriez-vous la méthode?
Merci d'avance.

[bastienbastoc]

Bonjour,
Il faut passer par les fonctions. Déjà on se doute bien que la suite est croissante . A ta place j'aurai étudié la fonction x^2+6 qui pour tout x est strictement plus grande que x. Alors en particulier pour x = Un aussi.

[Ben314]

Salut,
Perso, partant de l'inéquation (à confirmer/infirmer), c'est à dire , plutôt que de l'écrire qui n'avance à peu prés à rien, je l'aurais plutôt écrit sous la forme (*) qui est clairement vrai.
Bref, comme toujours, de passer de à ne doit pas être un automatisme : il y a (pas mal) de fois où c'est pertinent, mais bien évidement, il y a des cas comme ici où ça ne l'est pas du tout.

(*) Qui est équivalente à condition de savoir que .
Cela provient du fait que la fonction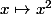 est strictement croissante sur donc deux nombres positifs sont dans le même ordre que leur carrés respectifs.

[pascal16]

suite au bug des formules latex

Un est définie car Un²+6 est positif

(Un+1)² = Un²+6
donc (Un+1)² >Un²
par stricte croissance de la fonction carré pour x>0, on a Un+1>Un

Un est définie et strictement croissante.

variante :
Un²= Un²
Un²+6>Un²
par croissance de la fonction racine bien définie
V(Un²+6) > V(Un)
par positivité de Un (marche même sans justifier ici)
V(Un²+6) > Un