utilisateura a écrit:Bonjour, j'aurai besoin d'aide pour l'exercice suivant :
A chaque nombre réel m, on associe la fonction fm définie sur ℝ par f m( x)=x^3+ m x^2+ m x+ 1
Déterminer les valeurs de m pour lesquelles la fonctions fm admet au moins deux extremums locaux.
Bon je vais t'expliquer petit à petit ce qui a déjà été dit plus haut (mais peut-être que ça a été trop rapide).
Ce qu'il faut comprendre, c'est que les
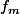
forment une famille de fonctions: ce n'est pas une seule fonction, mais selon la valeur de m, tu as une fonction différente.
Par exemple si m = 1,
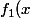 = x^3 + x^2 + x + 1)
Si m = 2,
 = x^3 + 2x^2 + 2x + 1)
Comme chaque fois que tu choisis un m différent, tu obtiens une fonction différente. Pour une fonction donnée, comme

par exemple si on veut trouver ses extrémas, on la dérive, non? On calcule sa dérivée et on repère en quels x on aurait
 = 0)
. Pour

toujours,
 = 3x^2 + 2x + 1)
. En calculant le discriminant, on trouve
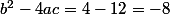
donc aucune racine réelle ! C'est à dire que

ne s'annule jamais... donc pour m = 1, on n'a pas deux extrémums locaux (on en a aucun, en fait)
Par contre, si tu prends par exemple m = 4, on a
=x^3+ 4 x^2+ 4 x+ 1)
 = 3x^2 + 8x + 4)
a pour discriminant
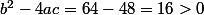
on a donc deux racines réelles pour la dérivée, elle s'annule deux fois et passe du positif au négatif en ces deux racines: alors m = 4 est une valeur pour laquelle f_m donc f_4 possède deux extrémums locaux.
Maintenant que tu as compris comment ça marche pour des valeurs de m choisies (on regarde la dérivée pour voir si delta est strictement positif, donc deux racines), tu peux essayer de raisonner dans le cas général:
Supposons qu'on ait m un nombre pour lequel
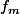
possède deux extrémas locaux.
Cela signifie que

s'annule deux fois.
Comme pour tout m,
=3x^2+ 2m x+ m)
, on doit avoir b^2 - 4ac > 0, soit
^2 - 4\times3\times m > 0)
C'est-à-dire que tu dois résoudre l'inéquation
^2 - 4\times3\times m > 0)
qui va te donner les valeurs de m pour lesquelles le discriminant est strictement positif. Pour ces m là, tu auras deux "x" (qui dépendent de ton choix de m à chaque fois) qui annulent la dérivée de fm et en lesquelles celle-ci change de signe, c'est à dire deux extrémas locaux au moins.
