Une famille de fonctions

par **Arnaud-29-31** » 12 Jan 2011, 22:07

Coucou !
La question c'est uniquement donner le nombre de solutions de

?
Parce que si c'est ça, c'est fini

par **Rebelle_** » 12 Jan 2011, 22:10

Oui c'est ça patate, je te l'ai dit rhooo :P
Non mais je voudrais aussi les trouver moi ^^' Tu vois, parce que j'aime bien me prouver que je suis une boulette :D

PS : coucou ? ^^ Oh, on est trop classique là :(

par **Arnaud-29-31** » 12 Jan 2011, 22:15

Et bé tu les as trouvé les racines bouriquette !

Y'en a pas pour

, ce sont

et

(oula zut on a divisé par qqch ca vaut pas zéro des fois ? ^^)

Maintenant si c'est leur signe que tu veux, tu as bien sur comme tu l'as dit

négative et regarde mieux

... vu ke k est forcément négatif ou nul ...

par **Rebelle_** » 12 Jan 2011, 22:17

Yes, mais on a

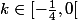
, comment peut-on être sûr que dans ces conditions les racines trouvées sont bien comprises dans ]0, + l'infini[ ?

Je suis fatiguée.....

Et ne balance pas mes surnoms, s'il te plait ^^' Vilain va.

par **Olympus** » 12 Jan 2011, 22:19

Salut Ju' !

Pour la fin, regarde ce qui se passe lorsque

, puis

( j'ai pas regardé ce qu'il y a avant désolé, je suis un petit peu occupé )

par **Rebelle_** » 12 Jan 2011, 22:21

Salut =)

Ben euh l'énoncé pose k un réel négatif :/ Tu veux quand même que je regarde ce que me dit Wolfram ? ^^'

par **Rebelle_** » 12 Jan 2011, 22:25

Arnaud-29-31 a écrit:(oula zut on a divisé par qqch ca vaut pas zéro des fois ? ^^)

Maintenant si c'est leur signe que tu veux, tu as bien sur comme tu l'as dit négative et regarde mieux ... vu ke k est forcément négatif ou nul ...

Non, on a posé k différent de 0 plus haut

L'ennui c'est que je sais que k est négatif, donc le dénominateur l'est mais je ne sais pas comment il se comporte par rapport au numérateur. Disons que j'ai la flemme de faire l'étude de signe avec la racine blabla. Dois-je ? :/

par **Olympus** » 12 Jan 2011, 22:26

Ha, j'ai bien dit que je n'ai pas lu ce qu'il y a avant :ptdr:

Sinon, c'est toujours la même méthode : multiplie par le conjugué :)

par **Rebelle_** » 12 Jan 2011, 22:28

Hum le conjugué, oulah que c'est ennuyant ça (a)
Je pense que je verrai ça demain matin :P

En tout cas merci pour votre aide à tous les deux !

Arnaud, va te coucher. :)

par **Arnaud-29-31** » 12 Jan 2011, 22:30

Rebelle_ a écrit:or n'admet de solution réelle que si c'est-à-dire et k différent de 0.

J'avais pas vu ça mais c'est faux ... y'a bien des solutions réelles pour k=0 et c'est un cas à mettre à part.

Et pour finir, tu ne peux pas aller plus loin que ça ...

pas de solution

une solution x_0 = 2

deux solutions

et

(qui est aussi négative puisque 1 + 4k < 1 puis

)

une solution

par **Rebelle_** » 12 Jan 2011, 22:31

Oui, pour k = 0 il y a x = 1....

par **Rebelle_** » 13 Jan 2011, 17:55

Re =)

Bon, je vais commencer par m'en tenir à l'énoncé ^^' On veut donc déterminer le nombre de racines de

pour x dans ]0, + l'infini[.
Puis-je dire que l'équation n'admet de solutions que si le discriminant associé est positif ou nul ? Si oui, je suis obligée de faire une étude de k, non (ahahah.) ?

par **fatal_error** » 13 Jan 2011, 18:03

yo,

Puis-je dire que l'équation n'admet de solutions que si le discriminant associé est positif ou nul ?

oui

Si oui, je suis obligée de faire une étude de k, non (ahahah.) ?

pour les deux solutions pour sassurer quelles sont bien positives, oui.

mais arnaud-29-31 tas fait letude. Le premier cas est trivial, tu las fait.
le second est fait par encadrement
-1/4<k<0
-1<4k<0
0<4k+1<1
0<sqrt(4k+1)<1
qui est l'inégalité proposé par arnaud-29-31 et qui de fait te donne le signe de -1+(sqrt(4k+1)) et à fortiori de x_2

par **Rebelle_** » 13 Jan 2011, 18:05

Hum d'accord merci beaucoup ! :)
Je vais rédiger tout ça proprement maintenant ^^'

Une famille de fonctions

Qui est en ligne