Une comparaison niveau 1ère S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
kabakas
- Membre Naturel
- Messages: 74
- Enregistré le: 20 Jan 2013, 20:39
-
 par kabakas » 29 Sep 2018, 12:54
par kabakas » 29 Sep 2018, 12:54
bonjour
une aide stp

merci
-
qaterio
- Membre Relatif
- Messages: 288
- Enregistré le: 22 Aoû 2018, 18:55
-
 par qaterio » 29 Sep 2018, 13:31
par qaterio » 29 Sep 2018, 13:31
j'ai pas trop réfléchi à ton problème, mais déjà, tu peux poser b=1-a, et après j'imagine que tu fais une petite récurrence...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 29 Sep 2018, 13:42
par Ben314 » 29 Sep 2018, 13:42
Salut,
Si tu sait ce qu'est une étude de fonction, on peut passer par là :
Pour

et

, on pose
\!=\!(1\!+\!x^{-n})(1\!+\!y^{-n}))
où
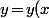\!=\!1\!-\!x)
donc
\!=\!-1)
.
=-nx^{-n-1}(1\!+\!y^{-n})+ny^{-n-1}(1\!+\!x^{-n})\cr\ \ \ \ \ \ \ \ <br />=nx^{-n-1}y^{-n-1}\big(x^{n+1}\!+\!x\!-\!y^{n+1}\!-\!y\big))
Or

est du signe de

(car
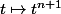
est croissante sur

) donc
)
est du signe de

ce qui signifie (tableau de variation) que le minimum de la fonction est obtenu pour

.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
