Bonjour
Juste une petite piste pour transformer acos(x)+bsin(x) dans le cas général.
Merci d'avance.
Trigonométrie acos(x) + bsin(x)
7 messages
- Page 1 sur 1
Re: Trigonométrie acos(x) + bsin(x)
Salut,
Il y a de multiples façons. Tout dépend de ce que tu veux faire.
Par exemple tu peux mettre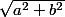 en facteur et exprimer
en facteur et exprimer 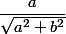 et
et 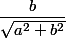 comme le cosinus et le sinus d'un angle
comme le cosinus et le sinus d'un angle  .
.
Il y a de multiples façons. Tout dépend de ce que tu veux faire.
Par exemple tu peux mettre
Re: Trigonométrie acos(x) + bsin(x)
Merci SaMajesté.
Justement il faut que 0<a/V(a²+b²)<=1 pour qu'il puisse sinus ou cosinus d'un réel.
Juste une petite piste pour le démontrer. Je savais le démontrer il y a x temps !
Je pense qu'il faut appliquer les fonctions carrée et inverse mais je n'y arrive pas.
Justement il faut que 0<a/V(a²+b²)<=1 pour qu'il puisse sinus ou cosinus d'un réel.
Juste une petite piste pour le démontrer. Je savais le démontrer il y a x temps !
Je pense qu'il faut appliquer les fonctions carrée et inverse mais je n'y arrive pas.
Re: Trigonométrie acos(x) + bsin(x)
Oui,
0<a²<=a²+b²
En divisant par a²+b² non nul:
0<a²/(a²+b²)<=1
Pour la forme: -1<a²/(a²+b²)<=1
Donc a²/(a²+b²) peu être le sinus ou le cosinus d'un réel.
0<a²<=a²+b²
En divisant par a²+b² non nul:
0<a²/(a²+b²)<=1
Pour la forme: -1<a²/(a²+b²)<=1
Donc a²/(a²+b²) peu être le sinus ou le cosinus d'un réel.
Re: Trigonométrie acos(x) + bsin(x)
Bien sûr, acos(x), bsin(x), donc prendre la racine carrée, c'est un oubli de notation.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
