Trigo/complexes DM pour prépa

par **Wingarsia** » 16 Aoû 2015, 18:28

Bonjour, je rentre en PCSI en septembre et j'ai un dm à faire pendant les vacances, il me reste un exercice que je n'arrive pas à résoudre.

On définit les nombres réels A et B par

En considérant au préalable le nombre complexe A+iB, calculer explicitement A.

Je ne sais pas trop quoi faire... j'avais pensé à écrire:

Je sais que le résultat est 1/2 mais je ne sais pas quoi faire à partir de là...

Merci de votre aide!

par **mathelot** » 16 Aoû 2015, 18:44

utiliser la notation d'Euler et la formule de De Moivre

par **Wingarsia** » 16 Aoû 2015, 19:05

mathelot a écrit:utiliser la notation d'Euler et la formule de De Moivre

J'ai utilisé la formule de De Moivre, j'arrive à ça

mais après?

par **chan79** » 16 Aoû 2015, 19:30

Wingarsia a écrit:J'ai utilisé la formule de De Moivre, j'arrive à ça

mais après?

salut
si tu poses

Calcule

et factorise

par **capitaine nuggets** » 16 Aoû 2015, 19:53

Salut !

Je te propose une autre méthode :

Puisque

(il s'agit de la somme des racines septièmes de l'unité dont les points correspondant aux affixes, représente un heptagone régulier centré en l'origine), on a :

[CENTER]

[/CENTER]

Donc

.

En justifiant que

,

et

, déduis-en qu'alors

.

:+++:

par **Wingarsia** » 16 Aoû 2015, 20:18

chan79 a écrit:salut
si tu poses

Calcule et factorise

Alors

, mais comment factoriser

?

par **Wingarsia** » 16 Aoû 2015, 20:21

capitaine nuggets a écrit:Salut !

Je te propose une autre méthode :

Puisque (il s'agit de la somme des racines septièmes de l'unité dont les points correspondant aux affixes, représente un heptagone régulier centré en l'origine), on a :

[CENTER][/CENTER]

Donc .

En justifiant que , et , déduis-en qu'alors .

:+++:

Merci de ta réponse, je n'y aurais pas pensé :++: je vais tout de meme essayer de le résoudre avec les indications de l'énoncé :lol3:

par **mathelot** » 16 Aoû 2015, 20:33

je t'ai demandé d'utiliser la notation d'Euler

c'est un gap entre le programme de TS et celui de prépa

par **chan79** » 16 Aoû 2015, 21:33

Wingarsia a écrit:mais comment factoriser ?

par **mathelot** » 17 Aoû 2015, 09:15

NB:

et

désignent la partie réelle et imaginaire d'un complexe

par **Wingarsia** » 17 Aoû 2015, 11:51

Merci, j'ai réussi l'exo

par **mathelot** » 17 Aoû 2015, 14:27

capitaine nuggets a écrit:[CENTER][/CENTER]

????????????

capitaine nuggets a écrit:En justifiant que

???????????????

par **capitaine nuggets** » 17 Aoû 2015, 14:30

capitaine nuggets a écrit:Salut !

Je te propose une autre méthode :

Puisque (il s'agit de la somme des racines septièmes de l'unité dont les points correspondant aux affixes, représente un heptagone régulier centré en l'origine), on a :

[CENTER][/CENTER]

Donc .

En justifiant que , et , déduis-en qu'alors .

:+++:

Salut !

Attention, je viens de me rendre compte que j'avais fait une erreur : en fait, j'ai calculé

...

J'aurais dû considérer la somme

dont les point images constituent un tétradécagone ...

Du coup, ne tiens pas compte de ma méthode, elle n'a pas l'air de fonctionner.

:cry:

par **mathelot** » 17 Aoû 2015, 14:33

en tous cas, les deux angles supplémentaires donnent

par **chan79** » 17 Aoû 2015, 15:07

La partie réelle est bien 1/2

par **mathelot** » 17 Aoû 2015, 16:56

chan79 a écrit:

La partie réelle est bien 1/2

il y a une coquille ligne 1: lire

par **chan79** » 17 Aoû 2015, 17:03

mathelot a écrit:il y a une coquille ligne 1: lire

Merci, j'ai corrigé
Tant qu'à faire, on en déduit aussi:

par **Doremifanny** » 23 Aoû 2015, 07:48

Bonjour, j'ai le même exercice à faire et je n'ai pas compris comment vous avez trouvé 1/2. Pouvez vous me détailler vos calculs svp ?

par **Carpate** » 23 Aoû 2015, 09:27

Doremifanny a écrit:Bonjour, j'ai le même exercice à faire et je n'ai pas compris comment vous avez trouvé 1/2. Pouvez vous me détailler vos calculs svp ?

Il me semble que les 2 méthodes exposées sont bien détaillées
Peux-tu indiquer tes calculs et ce qui te pose problème

par **mathelot** » 23 Aoû 2015, 12:41

Doremifanny a écrit:Bonjour, j'ai le même exercice à faire et je n'ai pas compris comment vous avez trouvé 1/2. Pouvez vous me détailler vos calculs svp ?

Les pré-requis pour comprendre l'une ou l'autre des deux méthodes est la connaissance
des racines de l'unité.

ce sont des complexes de module 1 , equi-répartis sur le cercle unité.

Leurs arguments trigonométriques sont en progression arithmétique
et ces racines sont, peu ou prou, en progression géométrique,
ce qui permet de sommer des cosinus comme partie réelle d'une somme de termes
complexes en progression géométrique .

Le deuxième pré-requis est la formule sommatoire

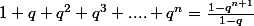
qu'on applique avec

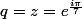
et

un troisième pré-requis est la formule de De Moivre

qu'on utilise via

la méthode de chan est meilleure que la mienne car il rejoint ce que l'on appelle la "présentation
d'un groupe (ici U_n, les racines n-ièmes de l'unité) par générateur et relations. "

Trigo/complexes DM pour prépa

Trigo/complexes DM pour prépa

pré-requis

Qui est en ligne