Trigo/complexes DM pour prépa
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Doremifanny
- Messages: 3
- Enregistré le: 23 Aoû 2015, 07:47
-
par Doremifanny » 24 Aoû 2015, 12:19
Merci beaucoup de la réponse!
Cependant je n'ai jamais entendu parler des racines de l'unité, j'ai recherché ça sur le web et les explications sont pas trop de mon niveau sortie terminale..
J'ai compris tous les calculs que vous avez fait jusqu'à cette partie là :
1 / (1 - cos(pi/7) - isin(pi/7)) = (1 - cos(pi/7) + isin(pi/7)) / (2 - 2cos(pi/7))
Ici, c'est l'incompréhension
-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
par capitaine nuggets » 24 Aoû 2015, 12:45
Les racines
-ièmes de l'unité sont les solutions complexes de l'équation
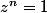
(il y en a exactement
, elle sont données par
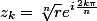
, où
).
Pour résoudre cette équation, pose
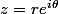
avec
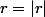
et
)
.
:+++:
-
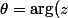Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
par Carpate » 24 Aoû 2015, 13:37
Doremifanny a écrit:Merci beaucoup de la réponse!
Cependant je n'ai jamais entendu parler des racines de l'unité, j'ai recherché ça sur le web et les explications sont pas trop de mon niveau sortie terminale..
J'ai compris tous les calculs que vous avez fait jusqu'à cette partie là :
1 / (1 - cos(pi/7) - isin(pi/7)) = (1 - cos(pi/7) + isin(pi/7)) / (2 - 2cos(pi/7))
Ici, c'est l'incompréhension
C'est une méthode classique que l'on rencontre dans tous les cours sur les nombres complexes.
Pour ne plus avoir de nombre complexe au dénominateur d'une expression, on multiplie numérateur et dénominateur de cette expression par la quantité conjuguée de son dénominateur.
Exemple :
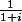
et
(1+i)=1-i^2=2)
(1+i)}=\frac{1-i}{2})
 - isin(\frac{\pi}{7})}=\frac{1 - cos( \frac{\pi}{7}) + isin(\frac{\pi}{7})} {(1 - cos(\frac{\pi}{7}) - isin(\frac{\pi}{7}))(1 - cos(\frac{\pi}{7}) + isin(\frac{\pi}{7}))}=\frac{1 - cos( \frac{\pi}{7}) + isin(\frac{\pi}{7})} {(1 - cos(\frac{\pi}{7}))^2 +sin^2(\frac{\pi}{7})}=\frac{1 - cos( \frac{\pi}{7}) + isin(\frac{\pi}{7})} {2(1- cos(\frac{\pi}{7}))})
-
mathelot
par mathelot » 24 Aoû 2015, 14:57
Carpate a écrit: (*)
La dernière étape est de considérer la partie réelle du dernier quotient (*).
Le dénominateur est réel.
on zappe tout ce qui est en i.
concernant la partie réelle, elle vaut 1/2
-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
par chan79 » 24 Aoû 2015, 15:03
-
Doremifanny
- Messages: 3
- Enregistré le: 23 Aoû 2015, 07:47
-
par Doremifanny » 25 Aoû 2015, 08:05
Merci beaucoup, j'étais tellement parti dans le compliqué que j'avais même pas pensé à multiplier par l'expression conjuguée :mur:
Bon maintenant je vais essayer de résoudre ça avec la racine n-ième :++:
-
mathelot
par mathelot » 25 Aoû 2015, 15:31
si tu continues le même exercice , ce sont des racines 14-ieme de l'unité
et aussi des racines 7-ieme de -1
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
