Bonjour;
j'aimerais avoir de l'aide pour une question en mathématique où je bloque la consigne suivante :
Démontrer que si n et k sont deux entiers tels que k≤ n-2, alors :
(n+2) = (n)+2( n )+ ( n )
(k+2) (k) (k+1) (k+2)
Je sais que je dois utiliser la formule suivante : (n) + ( n ) =(n+1)
(k) (k+1) (k+1)
Mais je ne parviens pas à l'utiliser.
Merci de votre aide
Triangle de Pascal
5 messages
- Page 1 sur 1
Re: Triangle de Pascal
Salut !
Remarque que :
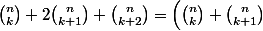 + \left( \binom n {k+1} + \binom n {k+2} \right)) .
.
Utilise alors ta formule pour exprimer ce qu'il y a dans les parenthèses : et
et  .
.
Tu obtiendras alors ainsi la somme de deux coefficients binomiaux. Il faudra encore utiliser ta formule.

Remarque que :
Utilise alors ta formule pour exprimer ce qu'il y a dans les parenthèses :
Tu obtiendras alors ainsi la somme de deux coefficients binomiaux. Il faudra encore utiliser ta formule.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Triangle de Pascal
Merci de ton aide;
J'ai fait ce que tu m'a dis mais je me retrouve avec : (n) -2(n+1) + ( n )
(k) (k+1) (k+2)
je ne pense pas que ça soit normal
J'ai fait ce que tu m'a dis mais je me retrouve avec : (n) -2(n+1) + ( n )
(k) (k+1) (k+2)
je ne pense pas que ça soit normal
Re: Triangle de Pascal
je pense être sur une piste mais j'aimerais avoir votre affirmation sur :
(n+1)= ( n ) + ( n )
(k+2) (k+1) (k+2)
Merci d'avance
(n+1)= ( n ) + ( n )
(k+2) (k+1) (k+2)
Merci d'avance
Re: Triangle de Pascal
Je ne comprends pas tes réponses...
Que vaut ?
?
Que vaut ?
?
Donc qu'en déduis-tu pour + \left( \binom n {k+1} + \binom n {k+2} \right)) ?
?
capitaine nuggets a écrit:Salut !
Remarque que :.
Utilise alors ta formule pour exprimer ce qu'il y a dans les parenthèses :et
.
Tu obtiendras alors ainsi la somme de deux coefficients binomiaux. Il faudra encore utiliser ta formule.
Que vaut
Que vaut
Donc qu'en déduis-tu pour
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 132 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
