DM théorème variations de f(x)=(u(x))²
14 messages
- Page 1 sur 1
DM théorème variations de f(x)=(u(x))²
Bonjour à tous, je bloque dans mon Dm qui est :
On considère une fonction u définie sur un intervalle I
La fonction f est donnée par f(x)=(u(x))²
1) Quel est l'ensemble de définition de f ? Justifier
2) Enoncer un théorème qui donne les variations de f en fonction du signe et des variations de u. Le démontrer avec soin
3) Appliquer ce théorème avec la fonction u(x)=(x-1)² - 2
Pour commencer l'ensemble de définition, logiquement c'est [0;+infini[ vu qu'on a un carré ?
Avec ce même carré je me dis que quand u est croissante, f l'est aussi
Que quand u est décroissante, f est croissante
Que quand u(x) est négatif, f(x) n'existe pas
Que quand u(x) est nul, f(x) l'est aussi
Que quand u(x) est positif f(x) l'est aussi
Donc deja, mes observations sont justes ? sinon merci de me corriger
Et si possible, si vous pouvez un peu m'aider pour la suite ou m'aider à trouver les réponses, je vous remercie vraiment
Merci beaucoup
On considère une fonction u définie sur un intervalle I
La fonction f est donnée par f(x)=(u(x))²
1) Quel est l'ensemble de définition de f ? Justifier
2) Enoncer un théorème qui donne les variations de f en fonction du signe et des variations de u. Le démontrer avec soin
3) Appliquer ce théorème avec la fonction u(x)=(x-1)² - 2
Pour commencer l'ensemble de définition, logiquement c'est [0;+infini[ vu qu'on a un carré ?
Avec ce même carré je me dis que quand u est croissante, f l'est aussi
Que quand u est décroissante, f est croissante
Que quand u(x) est négatif, f(x) n'existe pas
Que quand u(x) est nul, f(x) l'est aussi
Que quand u(x) est positif f(x) l'est aussi
Donc deja, mes observations sont justes ? sinon merci de me corriger
Et si possible, si vous pouvez un peu m'aider pour la suite ou m'aider à trouver les réponses, je vous remercie vraiment
Merci beaucoup
J'en arrive à
1. f(x) est aussi définie pour x élément de I. Car la fonction carré est définie sur R et u sur I, donc u^2 définie sur R inter I, soit I.
2. U positive et croissante->F positive et croissante
U positive et décroissante->F positive et décroissante
U négative et croissante->F positive et décroissante
U négative et décroissante->F positive et croissante
cependant je ne sais pas trop comment justifier, "démontrer avec soin" ce que je mets dans la 2
1. f(x) est aussi définie pour x élément de I. Car la fonction carré est définie sur R et u sur I, donc u^2 définie sur R inter I, soit I.
2. U positive et croissante->F positive et croissante
U positive et décroissante->F positive et décroissante
U négative et croissante->F positive et décroissante
U négative et décroissante->F positive et croissante
cependant je ne sais pas trop comment justifier, "démontrer avec soin" ce que je mets dans la 2
@Salawesh
Si la fonction est dérivable sur
est dérivable sur  alors la fonction
alors la fonction  est dérivable sur
est dérivable sur 
ET on a :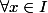
=2u'(x)u(x))
ET c'est "facile" de conclure sur la monotonie (sens de variation) de la fonction en étudiant le signe de
en étudiant le signe de ) sur
sur 
MAIS si la fonction n'est pas dérivable sur
n'est pas dérivable sur 
comment justifier correctement ? "une éventuelle monotonie" de la fonction définie par
définie par =(u(x))^2) quand
quand 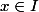
Si la fonction
ET on a :
ET c'est "facile" de conclure sur la monotonie (sens de variation) de la fonction
MAIS si la fonction
comment justifier correctement ? "une éventuelle monotonie" de la fonction
ptitnoir a écrit:On a :
car si le fonctionn'est pas définie alors la fonction
n'est pas définie
et on a en effet sialors
car .....
Je ne suis plus sûr de savoir ce que ca signifie :
Et la justification ce n'est pas ce que j'ai mis ? "Car la fonction carré est définie sur R et u sur I, donc u^2 définie sur R inter I, soit I. "
ptitnoir a écrit:@Salawesh
Si la fonctionest dérivable sur
alors la fonction
est dérivable sur
ET on a :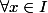
=2u'(x)u(x))
ET c'est "facile" de conclure sur la monotonie (sens de variation) de la fonctionen étudiant le signe de
sur
MAIS si la fonctionn'est pas dérivable sur
comment justifier correctement ? "une éventuelle monotonie" de la fonctiondéfinie par
Je comprends pas trop les dérivés, on a pas encore fait en fait, c'est la seule solution ?
OUI c'est OKSalawesh a écrit:Je ne suis plus sûr de savoir ce que ca signifie :
Et la justification ce n'est pas ce que j'ai mis ? "Car la fonction carré est définie sur R et u sur I, donc u^2 définie sur R inter I, soit I. "
Le domaine de définition de f est inclus dans le domaine de définition de u (car f est définie à partir de u)
ET tu as raison comme la fonction "carré" est définie sur IR
+ comme I est un intervalle de IR
on a bien
Salawesh a écrit:Bonjour à tous, je bloque dans mon Dm qui est :
On considère une fonction u définie sur un intervalle I
La fonction f est donnée par f(x)=(u(x))²
1) Quel est l'ensemble de définition de f ? Justifier
2) Enoncer un théorème qui donne les variations de f en fonction du signe et des variations de u. Le démontrer avec soin
3) Appliquer ce théorème avec la fonction u(x)=(x-1)² - 2
Pour commencer l'ensemble de définition, logiquement c'est [0;+infini[ vu qu'on a un carré ?
Avec ce même carré je me dis que quand u est croissante, f l'est aussi
Que quand u est décroissante, f est croissante
Que quand u(x) est négatif, f(x) n'existe pas
Que quand u(x) est nul, f(x) l'est aussi
Que quand u(x) est positif f(x) l'est aussi
Donc deja, mes observations sont justes ? sinon merci de me corriger
Et si possible, si vous pouvez un peu m'aider pour la suite ou m'aider à trouver les réponses, je vous remercie vraiment
Merci beaucoup
[FONT=Trebuchet MS]Un des Elèves de 1ère S2 à ce que je vois , tricher n'est pas jouer et l'on récolte ce que l'on sème.
Penser plutôt que le jour du contrôle , vous n'aurez pas accès à Maths-Forum '-'
[/FONT]
:marteau:
@RandAlThor
En quoi Salawesh a triché ?
Je ne comprends pas
- ni qui a écrit ce message
- ni le but de ce message
Questions :
est ce qu'un autre élève , qui est dans la même classe de Salawesh , et qui travaille ses maths le soir avec son grand frère, triche ?
est ce qu'un autre , qui prend des cours de maths particuliers , triche ?
est ce qu'un élève , pour faire son DM de maths , et qui demande de l'aide à un autre élève de sa classe , triche ?
En quoi Salawesh a triché ?
Je ne comprends pas
- ni qui a écrit ce message
- ni le but de ce message
Questions :
est ce qu'un autre élève , qui est dans la même classe de Salawesh , et qui travaille ses maths le soir avec son grand frère, triche ?
est ce qu'un autre , qui prend des cours de maths particuliers , triche ?
est ce qu'un élève , pour faire son DM de maths , et qui demande de l'aide à un autre élève de sa classe , triche ?
ptitnoir a écrit:@RandAlThor
En quoi Salawesh a triché ?
Je ne comprends pas
- ni qui a écrit ce message
- ni le but de ce message
Questions :
est ce qu'un autre élève , qui est dans la même classe de Salawesh , et qui travaille ses maths le soir avec son grand , triche ?
est ce qu'un autre , qui prend des cours de maths particuliers , triche ?
est ce qu'un élève , pour faire son DM de maths , et qui demande de l'aide à un autre élève de sa classe , triche ?
Voilà un message pertinent
Par contre, il est vrai qu'un élève qui ne demande que les réponses triche. Ici, je vois quelqu'un qui a le soucis de comprendre la façon dont mener ses exos.
salut RandAlThorRandAlThor a écrit:[FONT=Trebuchet MS]Un des Elèves de 1ère S2 à ce que je vois , tricher n'est pas jouer et l'on récolte ce que l'on sème.
Penser plutôt que le jour du contrôle , vous n'aurez pas accès à Maths-Forum '-'
[/FONT]
:marteau:
Qu'est ce que Salawesh a récolté à son dernier contrôle de maths ?
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 126 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
