Théorème des restes chinois

[dd07]

Bonjour,
Je suis bloqué sur un exercice depuis plusieurs heure déjà :
Enoncé : Une bande de 17 pirates possède un trésor constitué de pièces d’or d’égale valeur. Ils projettent de se les partager également, et de donner le reste au cuisinier chinois. Celui- ci recevrait alors 3 pièces. Mais les pirates se querellent, et six d’entre eux sont tués. Un nouveau partage donnerait au cuisinier 4 pièces. Dans un naufrage ultérieur, seuls le trésor, six pirates et le cuisinier sont sauvés, et le partage donnerait alors 5 pièces d’or à ce dernier. Quelle est la fortune minimale que peut espérer le cuisinier s’il décide d’empoisonner le reste des pirates ?"

j'ai commencé à écrire ce système
N=3 + 17k
N= 4 + 11k
N= 5+ 6k

Mais je n'arrive pas à résoudre ce système, et après je ne sais pas quoi faire
Merci de votre aide par avance

[hdci]

Bonjour,

Qui vous dit que dans les 3 cas, chaque pirate survivant reçoit la même quantité ? Vous avez utilisé la même inconnue k, alors qu'en fait c'est k, k' et k'' qu'il faut écrire.

Ensuite, en écrivant N=3+17k=4+11k', vous en déduisez que 17k=1+11k' ; de même avec 3+17k=5+6k'', cela fait 17k=2+6k'' et finalement vous obtenez
1+11k'=2+6k''

C'est-à-dire
11k'=1+6k''.

Donc est divisible par 11 soit donc ce qui vous permet d'en déduire où a est un certain entier.

D'où avec , vous en tirez d'où est divisible par 17 (à vous de faire les calculs intermédiaires pour vérifier ce résultat)

c'est-à-dire

or l'inverse de 11 est 14 modulo 17, donc

Bref, en prenant a=11 la plus petite valeur possible (à vous de vérifier qu'avec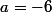 on obtient des quantités négatives), on obtient... (je vous laisse finir)