Bonjour.
Je bloque sur un exercice de maths. Voici l'énoncé:
On considère les suites u et v définies par:
u0=20 , v0=80 , u(n+1)=(2un+vn)/4 , v(n+1)=(un+2vn)/4
1) Calculer u1, v1, u2 et v2
J'ai trouvé u1=30, v1=45, u2=26.25, v2=30
2) Prouver que les suites (un+vn) et (vn-un) sont géométriques
J'ai trouvé (un+vn)=(3u(n-1)+3v(n-1))*1/4 et (vn-un)=(-1u(n-1)+3v(n-1))*1/4
3) Exprimer un+vn et vn-un en fonction de n
4) En déduire l'expression de un et vn en fonction de n puis calculer u2 et v2
5) Déterminer lim un et lim vn quand n -> +infini
Je bloque à partir de la question 3 et je pense avoir besoin de celle ci pour répondre à la 4 et à la 5. Je ne vois pas comment exprimer ces suites en fonction de n malgré mes recherches. Ai-je fait une erreur à la question précédente ? Comment exprimer ces suites en fonction de n ?
Merci d'avance.
PS: les equations LaTeX ne fonctionnent toujours pas pour moi
Terminale / Exprimer un + vn en fonction de n
11 messages
- Page 1 sur 1
Re: Terminale / Exprimer un + vn en fonction de n
Tu as trouvé : 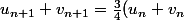)
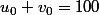
Tu ne sais pas exprimer le nième terme de la suite géométrique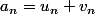 de raison
de raison 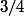 et de premier terme 100 en fonction de n ?
et de premier terme 100 en fonction de n ?
Tu ne sais pas exprimer le nième terme de la suite géométrique
Re: Terminale / Exprimer un + vn en fonction de n
Carpate a écrit:Tu as trouvé :
Tu ne sais pas exprimer le nième terme de la suite géométriquede raison
et de premier terme 100 en fonction de n ?
Vu comme ça je dirais
Re: Terminale / Exprimer un + vn en fonction de n
Non
Il faut exprimer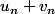 en fonction de
en fonction de 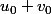 .
.
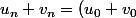(\frac34)^n)
Il faut exprimer
Modifié en dernier par Carpate le 03 Jan 2021, 16:09, modifié 3 fois.
Re: Terminale / Exprimer un + vn en fonction de n
Carpate a écrit:Non
Il faut exprimeren fonction de
.
Si tu jettes un regard à ton cours tu verras que le nième terme d'une suite géométriquede raison
et de premier terme
est
Donc je devrais obtenir
Re: Terminale / Exprimer un + vn en fonction de n
Confusion de ma part : J'ai édité mon message précédent et corrigé mon erreur ce n'est pas la somme des termes mais le nième terme
donc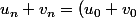 (\frac34)^n)
donc
Re: Terminale / Exprimer un + vn en fonction de n
Carpate a écrit:J'ai édité mon message précédent et corrigé mon erreur ce n'est pas la somme des termes mais le nième terme
donc
Merci beaucoup ! j'imagine que la relation est la même pour vn-un à condition qu'on change u0+v0 par v0-u0.
J'imagine également que pour la question 4) En déduire l'expression de un et vn en fonction de n je n'ai qu'à faire cela:
Re: Terminale / Exprimer un + vn en fonction de n
Non
u_n et v_n ne sont pas des suites géométrique mais u_n+v_n et u_n - v_n le sont
u_n et v_n ne sont pas des suites géométrique mais u_n+v_n et u_n - v_n le sont
Re: Terminale / Exprimer un + vn en fonction de n
Carpate a écrit:Non
u_n et v_n ne sont pas des suites géométrique mais u_n+v_n et u_n - v_n le sont
Comment déduire un et vn dans ce cas ?
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
