DM sur les complexes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 15 Déc 2012, 16:24
par Anonyme » 15 Déc 2012, 16:24
@mella12 et @Xulthiar
si on pose
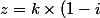)
avec
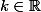
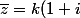)
et donc
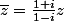 donc il existe d'autres solutions z=0 !
donc il existe d'autres solutions z=0 !
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 16:31
par Xulthiar » 15 Déc 2012, 16:31
Tu as :
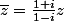
D'où :
}{1-i})
-2x+2iy}{2}=0)
Travaille à partir de cette équation. Je te donnerai la suite si besoin.
-
Anonyme
 par Anonyme » 15 Déc 2012, 16:40
par Anonyme » 15 Déc 2012, 16:40
Xulthiar a écrit:Tu as :
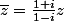
D'où :
}{1-i})
-2x+2iy}{2}=0)
Travaille à partir de cette équation. Je te donnerai la suite si besoin.
c'est n'importe quoi !!D'où vient le }{1-i}) ??
??
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 16:41
par mella12 » 15 Déc 2012, 16:41
ptitnoir a écrit:c'est n'importe quoi !!
D'où vient le }{1-i}) ??
??
Non non il a raison ! Peut être que tu as pas vu la multiplication par z à droite ..
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 16:42
par Xulthiar » 15 Déc 2012, 16:42
ptitnoir a écrit:c'est n'importe quoi !!
D'où vient le }{1-i}) ??
??
=\frac{(1+i)(x+iy)}{1-i}=\frac{x-y+ix+iy}{1-i})
-
Anonyme
 par Anonyme » 15 Déc 2012, 16:44
par Anonyme » 15 Déc 2012, 16:44
@mella12
bof bof bof car 
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 16:44
par mella12 » 15 Déc 2012, 16:44
J'ai refais le calcul du début et oui je m'étais trompé en développant au dénominateur et là je suis à

et il faut que je multiplie par le conjugué mais au dénominateur je multiplie quoi par le conjugué ? Tout ?
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 16:45
par mella12 » 15 Déc 2012, 16:45
Oui comme ça Xulthiar !
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 16:48
par Xulthiar » 15 Déc 2012, 16:48
mella12 a écrit:J'ai refais le calcul du début et oui je m'étais trompé en développant au dénominateur et là je suis à
\frac{x-y-x+i(x-y+y}{1-i} et il faut que je multiplie par le conjugué mais au dénominateur je multiplie quoi par le conjugué ? Tout ?
Tu multiplies par le conjugué au dénominateur et au numérateur.
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 16:50
par mella12 » 15 Déc 2012, 16:50
Xulthiar a écrit:Tu multiplies par le conjugué au dénominateur et au numérateur.
)(1+i)}{(1-i)(1+i)})
Comme ça ? Mais si je développe en haut ça va être n'importe quoi non ? lol
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 16:52
par Xulthiar » 15 Déc 2012, 16:52
mella12 a écrit:)(1+i)}{(1-i)(1+i)})
Comme ça ? Mais si je développe en haut ça va être n'importe quoi non ? lol
C'est effectivement un peu le bazar (c'est le soucis de cette méthode, elle nécessite quelques calculs)
Cependant, tu te débarrasses du

au dénominateur, et c'est le plus important.
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 17:02
par mella12 » 15 Déc 2012, 17:02
Xulthiar a écrit:C'est effectivement un peu le bazar (c'est le soucis de cette méthode, elle nécessite quelques calculs)
Cependant, tu te débarrasses du

au dénominateur, et c'est le plus important.
Je crois que j'ai une erreur (encore) donc je vais détailler au maximum mon calcul :
)(1+i)}{2})
(1+i)}{2})

}{2})
Voilà sur quoi je tombe.. :hum:
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 17:10
par Xulthiar » 15 Déc 2012, 17:10
Je ne sais pas si la fraction de départ est exacte (il me faudrait l'autre bout de l'égalité pour le savoir), mais partons de celle la.
Le passage de la deuxième ligne à la troisième est faux :
(1+i)}{2})
C'est :
+i(x-y-x+ix-iy+iy)}{2})
Et non

Et franchement, quand tu as

, simplifie, ça fait 0, ne les laisses pas comme ça, ça complique le calcul.
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 17:19
par mella12 » 15 Déc 2012, 17:19
Au départ ? J'avais

Et à la fin j'arrive à
}{2}=0)
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 17:21
par Xulthiar » 15 Déc 2012, 17:21
Tu as encore un dernier problème de signe pour la partie imaginaire (tu dois trouver
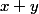
) et tu peux multiplier par 2 pour te débarrasser de la fraction et tu seras apte à conclure.
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 17:30
par mella12 » 15 Déc 2012, 17:30
Xulthiar a écrit:Tu as encore un dernier problème de signe pour la partie imaginaire (tu dois trouver
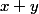
) et tu peux multiplier par 2 pour te débarrasser de la fraction et tu seras apte à conclure.
Je vois pas comment trouver x+y, quand je développe tout j'arrive à

Et en simplifiant tout je trouve l'expression que j'ai mise avant.
-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 17:34
par Xulthiar » 15 Déc 2012, 17:34
Tu es parti de cette fraction je suppose:
)(1+i)}{2})
Comment y es-tu arrivé ?
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 17:36
par mella12 » 15 Déc 2012, 17:36
En développant ceci

-
Xulthiar
- Membre Naturel
- Messages: 59
- Enregistré le: 07 Déc 2012, 22:36
-
 par Xulthiar » 15 Déc 2012, 17:40
par Xulthiar » 15 Déc 2012, 17:40
Non, ça c'est l'étape d'après.
Déjà, à quoi est égale cette fraction ? inclue-t-elle le
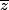
?
-
mella12
- Membre Relatif
- Messages: 184
- Enregistré le: 29 Oct 2012, 15:54
-
 par mella12 » 15 Déc 2012, 17:50
par mella12 » 15 Déc 2012, 17:50
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
au dénominateur, et c'est le plus important.
) et tu peux multiplier par 2 pour te débarrasser de la fraction et tu seras apte à conclure.