Salut, pourriez-vous me corriger mes erreurs SVP.
Un jardinier a planté 15 citronniers au printemps.Il estime que chacun d'entre eux a une probabilité de 60% de passer le premier hiver, indépendamment des autres.
1) Soit X le nombre de citronniers qui passera l'hiver, quelle est la loi de X ?
2) 5 citronniers viennent d'Espagne, et 10 du Maroc.Le jardinier observe que parmi les citronniers ayant passé l'hiver, 70% viennent du Maroc.
Déduisez-en la probabilité qu'un citronnier passe l'hiver sachant qu'il vient d'Espagne?
3) L'année suivante, le jardinier rachète 15 citronniers au hasard, il sait juste que chaque citronnier a 2 chances sur 3 de venir du Maroc.
Soit Z le nombre de citronniers qui viennent du Maroc et qui passent l'hiver.
Quelle est la loi de Z?
1) X suit la loi Binomial de paramètre n=15, et p=0,6
2) Avec la loi de Bayes:
Notons les événement suivant:
M: "provenance du Maroc"
E: "provenance d'Espagne"
H: "probabilité de passer l'Hiver"
P(H|E)= ( P(E|H) P(H) ) / P(E)
= ( P(E|H) P(H) ) / P(E|H) P(H) + P(E|H^c) P(H^c)
= (0,3 . 0,6) / ( 0,3 . 0,6 + 0,7 . 0,4) =0,39
la probabilité est de 39%
3) Z suit la loi géométrique de paramètre p=2/3
Sujet Probabilité
6 messages
- Page 1 sur 1
Re: Sujet Probabilité
2)
Je n'aime pas les probabilités ... et n'utilise quasi jamais les méthodes enseignées.
De plus, faire des calculs de probabiltés à partir d'échantillons aussi petits ne me semble pas bien raisonnable.
Il n'empêche, pour la question 2, je trouve une proba de 54 % pour qu'un citronnier venant d'Espagne passe l'hiver.
Et ... pas demandé, je trouve :
une proba de 63 % pour qu'un citronnier venant du Maroc passe l'hiver.
Pour moi (bien que ce genre de calculs ne devrait pas être faits ... si échantillons de tailles convenables) :
Sur 5 citronniers espagnol achetés, 2,7 citronniers passeront l'hiver et 2,3 citronniers vont crever.
Sur 10 citronniers marocains achetés, 6,3 citronniers passeront l'hiver et 3,7 citronniers vont crever.
Il y a donc 2,7 + 6,3 = 9 citronniers sur 15 qui passeront le 1er hiver (soit donc bien 60 % comme donné dans l'énoncé)
Et sur ces 9 citronniers qui ont passé l'hiver, il y en a 6,3 du Maroc (soit donc bien 100 * 6,3/9 = 70 % comme donné dans l'énoncé)
Les nombres décimaux, dans les résultats ci-dessus, qu'on ne peut pas arrondir à l'unité sans faire de grosses erreurs tentent à montrer que les échantillons (5 et 10 pièces) sont trop petits pour faire des calculs de probabilités sensés à partir d'une seule expérience.
Attendre la réponse d'un vrai matheux... mais avec un bon esprit critique.

Je n'aime pas les probabilités ... et n'utilise quasi jamais les méthodes enseignées.
De plus, faire des calculs de probabiltés à partir d'échantillons aussi petits ne me semble pas bien raisonnable.
Il n'empêche, pour la question 2, je trouve une proba de 54 % pour qu'un citronnier venant d'Espagne passe l'hiver.
Et ... pas demandé, je trouve :
une proba de 63 % pour qu'un citronnier venant du Maroc passe l'hiver.
Pour moi (bien que ce genre de calculs ne devrait pas être faits ... si échantillons de tailles convenables) :
Sur 5 citronniers espagnol achetés, 2,7 citronniers passeront l'hiver et 2,3 citronniers vont crever.
Sur 10 citronniers marocains achetés, 6,3 citronniers passeront l'hiver et 3,7 citronniers vont crever.
Il y a donc 2,7 + 6,3 = 9 citronniers sur 15 qui passeront le 1er hiver (soit donc bien 60 % comme donné dans l'énoncé)
Et sur ces 9 citronniers qui ont passé l'hiver, il y en a 6,3 du Maroc (soit donc bien 100 * 6,3/9 = 70 % comme donné dans l'énoncé)
Les nombres décimaux, dans les résultats ci-dessus, qu'on ne peut pas arrondir à l'unité sans faire de grosses erreurs tentent à montrer que les échantillons (5 et 10 pièces) sont trop petits pour faire des calculs de probabilités sensés à partir d'une seule expérience.
Attendre la réponse d'un vrai matheux... mais avec un bon esprit critique.
Re: Sujet Probabilité
Bonjour Black Jack,
Je suis parfaitement d'accord avec tout ce que tu dis. D'abord la petitesse de l'échantillon et ensuite le problème d'arrondi. En fait, ce chapitre des probabilités est utilisé comme support d'exercice de calcul et peut-être un peu de raisonnement. Ce n'est même pas de l'analyse combinatoire. D'ailleurs on a inventé le fameux "sachant que" qui a ouvert un champ magnifique. Je me souviens d'un bandit en fuite qui avait une probabilité de 10% de se cacher dans le bois. La bande de 30 maisons était fouillée par les services de police, on en était à la 30è maison. Question "quelle est la probabilité que le bandit soit dans cette maison ?".
Par contre la connaissance des probabilités, les vraies, est nécessaire dans notre monde moderne, mais c'est un autre débat.
Je suis parfaitement d'accord avec tout ce que tu dis. D'abord la petitesse de l'échantillon et ensuite le problème d'arrondi. En fait, ce chapitre des probabilités est utilisé comme support d'exercice de calcul et peut-être un peu de raisonnement. Ce n'est même pas de l'analyse combinatoire. D'ailleurs on a inventé le fameux "sachant que" qui a ouvert un champ magnifique. Je me souviens d'un bandit en fuite qui avait une probabilité de 10% de se cacher dans le bois. La bande de 30 maisons était fouillée par les services de police, on en était à la 30è maison. Question "quelle est la probabilité que le bandit soit dans cette maison ?".
Par contre la connaissance des probabilités, les vraies, est nécessaire dans notre monde moderne, mais c'est un autre débat.
Re: Sujet Probabilité
Commencons par résumer les donnée de l'énoncé :
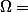

=0,6)
=\frac{1}{3})
=\frac{2}{3})
=0,7)
A partir de là, on peut :
- faire des arbres pondérés (je recommande, mais je ne le ferais pas ici, trop dur à dessiner)
- faire un tableau à deux entrée
- calculer de façon formelle
Commencons par le tableau :

De plus, = p(H) p_H(M) = 0,6 \times 0,7 = 0,42)

On peut ainsi compléter le tableau assez facilement :

On peut enfin répondre à la question posée : = \dfrac{p(EH)}{p(E)} = \frac{0,18}{1/3} = 0,54)
Il y a 54% de chances qu'un citronnier venant d'Espagne passe l'hiver
A partir de là, on peut :
- faire des arbres pondérés (je recommande, mais je ne le ferais pas ici, trop dur à dessiner)
- faire un tableau à deux entrée
- calculer de façon formelle
Commencons par le tableau :
De plus,
On peut ainsi compléter le tableau assez facilement :
On peut enfin répondre à la question posée :
Il y a 54% de chances qu'un citronnier venant d'Espagne passe l'hiver
Re: Sujet Probabilité
Salut,
Oui, résultat conforme au mien (54 %), obtenu pour ma part via un diagramme de Venn.
Ce résultat reste cependant très largement sujet à discussion en pratique pour les raisons que j'ai mentionnées.
L'énoncé ne permet pas un calcul satisfaisant sur une seule expérience à cause des échantillons beaucoup trop petits.

Oui, résultat conforme au mien (54 %), obtenu pour ma part via un diagramme de Venn.
Ce résultat reste cependant très largement sujet à discussion en pratique pour les raisons que j'ai mentionnées.
L'énoncé ne permet pas un calcul satisfaisant sur une seule expérience à cause des échantillons beaucoup trop petits.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
