Dm suites et récurrence
24 messages
- Page 1 sur 2 - 1, 2
Dm suites et récurrence
Bonjour à tous , voilà pour lundi j'ai un exercice noté à propos des suites et récurrence , mais j'ai des doutes je vais vous donner l'énoncé et comme je voudrais éviter de faire fausse route, j'aimerai quelques conseils avisés. Alors on considère la suite (Un) définie pour tout n de N par U0=3 et Un+1=4Un-2/x+1
1.Soit f la fonction définie sur [1;+infini[ par f(x)=4x-2/x+1
a. étudier les variations de f sur [1;+infini[
ici j'ai supposée qu'il fallait calculer tout d'abord la dérivé qui ici est u/v donc uv'-u'v/v2
dites moi si je me trompe , et dans ce cas on arrive à 6/(x+1)au carré mais je n'en suis pas sur et après établir un tableau de signe dont je suis peu sur aussi.
b. En déduire que, pour tout x de [1;+infini[, f(x) >ou égal à 1
des conseils ?
voilà pour le reste je pense être en mesure d'en venir à bout mais j'espère ne pas faire fausse route merci d'avance pour vos précieux conseils aguéries
1.Soit f la fonction définie sur [1;+infini[ par f(x)=4x-2/x+1
a. étudier les variations de f sur [1;+infini[
ici j'ai supposée qu'il fallait calculer tout d'abord la dérivé qui ici est u/v donc uv'-u'v/v2
dites moi si je me trompe , et dans ce cas on arrive à 6/(x+1)au carré mais je n'en suis pas sur et après établir un tableau de signe dont je suis peu sur aussi.
b. En déduire que, pour tout x de [1;+infini[, f(x) >ou égal à 1
des conseils ?
voilà pour le reste je pense être en mesure d'en venir à bout mais j'espère ne pas faire fausse route merci d'avance pour vos précieux conseils aguéries
Re: Dm suites et récurrence
Lulumineon a écrit:1.Soit f la fonction définie sur [1;+infini[ par f(x)=4x-2/x+1
Bonjour,
Avant de se lancer dans les calculs, soyons d'accord sur l'écriture de la fonction :
Est ce bien ceci ?
Re: Dm suites et récurrence
Dans ce cas, votre résultat est correct mais pourquoi en doutez vous ?
Est ce le calcul de la dérivée qui est "trop" calculatoire et donc source d'erreur ?
Est ce le calcul de la dérivée qui est "trop" calculatoire et donc source d'erreur ?
Re: Dm suites et récurrence
Pour être sur enfaite et le tableau de signe ça donnerai une fonction strictement positive car c'est un carré c'est cela ?
Re: Dm suites et récurrence
f est croissante sur
le tableau de variations montre que
Re: Dm suites et récurrence
Exact, la dérivée étant positive pour tout  différent de
différent de ) , votre fonction
, votre fonction  est croissante.
est croissante.
Sur votre intervalle d'observation,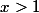 donc la valeur "interdite"
donc la valeur "interdite" 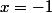 ne nous gène pas !
ne nous gène pas !
Concernant le calcul de la dérivée, il est possible de simplifier son calcul en transformant l'expression de départ=\frac{4x-2}{x+1}) en
en =a-\frac{b}{x+1}) ou
ou  et
et  sont deux nombres à trouver (par identification ça se fait les doigts dans le nez)
sont deux nombres à trouver (par identification ça se fait les doigts dans le nez) 
Sur votre intervalle d'observation,
Concernant le calcul de la dérivée, il est possible de simplifier son calcul en transformant l'expression de départ
Re: Dm suites et récurrence
Je vois, c'est plutôt ingénieux Anthony et dans ce cas là dans mon tableau de variation étant donné mon intervalle donné je n'ai pas à inscrire -1 et donc dans mon tableaux seront inscrit seulement -infini et 1 et une courbe croissante ci dessous ainsi que x+1 à gauche c'est cela ? est-il plus judiieux de ma part de la mettre sous la forme que vous m'avez proposé ? 
Re: Dm suites et récurrence
je ne comprend pas pourquoi lorsque x tend vers l'infini alors f(x) tend vers 4 et ducoup ce que je dois inscrire dans mon tableau :S
Re: Dm suites et récurrence
Lulumineon a écrit:je ne comprend pas pourquoi lorsque x tend vers l'infini alors f(x) tend vers 4 :S
C'est précisément pour cette raison (+une autre) que je vous suggérais de réécrire
Re: Dm suites et récurrence
Je vous propose dans un premier temps de trouver les nombres  et
et  pour réécrire
pour réécrire ) et après on va éclaircir tout ça !
et après on va éclaircir tout ça !
Re: Dm suites et récurrence
elle vaut 4 car on prend le terme possédant le plus haut degré nan? merci beaucoup pour votre patience
Re: Dm suites et récurrence
Si vous procédez ainsi c'est que vous n'avez pas calculé la limite à partir de la nouvelle forme de f(x) que je vous proposais 

Re: Dm suites et récurrence
Ah désolé j'ai du mal comprendre mais comment calculez vous la limite à partir de la nouvelle forme de f(x) , c'est que je me mélange un peu les pinceaux 
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 85 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
