Suites géométriques 1 ere S

[pbongrand]

bonjour je voulais savoir comment je peut résoudre un tel exercice car je ne sais pas comment faire pour trouver vn alors que je n'ai rien…

l'énoncé:

La suite (vn)n;)0 est une suite géométrique de raison q. Exprimer vn en fonction de n et calculer v20.
a. v1 = 1 et q = 3
b. v5 = 2 et q = -1
c. v50 = 1 024 et q = -2.

Desoler normalement je mets toujours le travail que j'ai fait mais la je ne vois pas comment le faire… si quelqu'un a une idée svp

merci d'avance

[pbongrand]

Je sais juste que
Si on a v0 : v_n=v0 q^n
Si on n'a pas v_0 mais une valeur vp pour un autre rang p : vn=vp q^{n-p}

Dans mon cas je dois utiliser la deuxième formule je pense mais je ne sais pas comment faire pour avoir la valeur de p

[Carpate]

Je sais juste que
Si on a v0 : v_n=v0 q^n
Si on n'a pas v_0 mais une valeur vp pour un autre rang p : vn=vp q^{n-p}

Dans mon cas je dois utiliser la deuxième formule je pense mais je ne sais pas comment faire pour avoir la valeur de p

[Slaker]

Salut !
Il y a même plus simple que la 2e formule, même si ça revient à la même chose :


Or la tu connais la valeur de v_1 et la valeur de q donc :



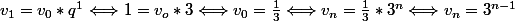
Ce qui te permet de facilement calculer v20

[Carpate]

Salut !
Il y a même plus simple que la 2e formule, même si ça revient à la même chose :


Or la tu connais la valeur de v_1 et la valeur de q donc :



Ce qui te permet de facilement calculer v20

Il me semble que tu écris exactement la même chose
P.S. Le signe d'équivalence n'est pas conseillé quand il s'agit de simples égalités

[pbongrand]

Merci mais comment je fais pour les autres ?? Parce que je comprend pas comment tu as fait

[Carpate]

Merci mais comment je fais pour les autres ?? Parce que je comprend pas comment tu as fait

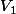
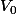
Connaissant et on en déduit par la relation
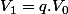
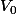
et étant connus, on obtient n par la relation
Et si tu refaisais toi-même ces calculs (avant d'écrire que tu ne comprends pas) ?

[pbongrand]

Je ne les ai pas encore écris je cherche d'abord a comprendre pour le jour du test le reste c'est pas majeure
Mais je crois que j'ai compris grâce a ces explications
je te donne les résultats que j'ai trouver pour les suivants:

[Slaker]

Il me semble que tu écris exactement la même chose
P.S. Le signe d'équivalence n'est pas conseillé quand il s'agit de simples égalités

Effectivement, le temps que je finisse d'écrire en Latex que tu avais déjà fini d'écrire.
J'ai mis les équivalences aussi à cause de Latex, mais c'est vrai que c'est superflu et que ça peut parfois être faux.

[pbongrand]

a)
Soit V20=3^19
soit 1162261467

[Carpate]

a)
Soit V20=3^19
soit 1162261467

Ma calculette trouve le même entier ...

[pbongrand]

Mais je n'ai pas de formule pour le b) Sachant que j'ai v5 et pas v1 ...

[Carpate]

Mais je n'ai pas de formule pour le b) Sachant que j'ai v5 et pas v1 ...

Où ets le problème ?

tu connais et ...
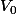
donc puis

[pbongrand]

Ah okk j'ai saisi

[pbongrand]

V0= -2
vn=2

[pbongrand]

vn=-2.-1^n

[pbongrand]

J'ai trouver pour v20=2
mes résultats sont ils correctes?

[Carpate]

V0= -2 Oui
vn=2

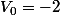
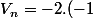Non


n pair
n impair

[pbongrand]

v0=(1024)/(-1,12589991.10^15)
vn=((1024)/(-1,12589991.10^15)) -2^n
v20=-1,09951268.10^12

[pbongrand]

oui j'ai confondu vn et v20 quand je l'ai marquer c'est pour ça que apres je me suis corrige. sinon les derniers calculs sont bons ?